Las traducciones son generadas a través de traducción automática. En caso de conflicto entre la traducción y la version original de inglés, prevalecerá la version en inglés.

Control de pulsos en Amazon Braket

Los pulsos son las señales analógicas que controlan los qubits en una computadora cuántica. Con algunos dispositivos de Amazon Braket, puede acceder a la característica de control de pulsos para enviar circuitos mediante pulsos. Puedes acceder al control de pulsos a través del SDK de Braket, mediante OpenQASM 3.0, o directamente a través del Braket. APIs En primer lugar, introduzca algunos conceptos clave para el control de pulsos en Braket.

Marcos

Un marco es una abstracción de software que actúa como un reloj dentro del programa cuántico y como una fase. La hora del reloj se incrementa con cada uso y con cada señal portadora con estado que se define mediante una frecuencia. Al transmitir señales al qubit, un marco determina la frecuencia portadora del qubit, el desplazamiento de fase y el momento en que se emite la envolvente de la forma de onda. En Braket Pulse, la construcción de marcos depende del dispositivo, la frecuencia y la fase. Según el dispositivo, puede elegir un marco predefinido o crear instancias de marcos nuevos proporcionando un puerto.

from braket.aws import AwsDevice
from braket.pulse import Frame, Port

# Predefined frame from a device
device = AwsDevice("arn:aws:braket:us-west-1::device/qpu/rigetti/Ankaa-3")
drive_frame = device.frames["Transmon_5_charge_tx"]

# Create a custom frame
readout_frame = Frame(frame_id="r0_measure", port=Port("channel_0", dt=1e-9), frequency=5e9, phase=0)

Puertos

Un puerto es una abstracción de software que representa cualquier componente de input/output hardware que controle los qubits. Ayuda a los proveedores de hardware a proporcionar una interfaz con la que los usuarios pueden interactuar para manipular y observar los qubits. Los puertos se caracterizan por una cadena única que representa el nombre del conector. Esta cadena también expone un incremento de tiempo mínimo que especifica la precisión con la que podemos definir las formas de onda.

from braket.pulse import Port

Port0 = Port("channel_0", dt=1e-9)

Formas de onda

Una forma de onda es una envolvente dependiente del tiempo que podemos utilizar para emitir señales en un puerto de salida o capturar señales a través de un puerto de entrada. Puede especificar sus formas de onda directamente, ya sea mediante una lista de números complejos o utilizando una plantilla de forma de onda para generar una lista del proveedor de hardware.

from braket.pulse import ArbitraryWaveform, ConstantWaveform
import numpy as np

cst_wfm = ConstantWaveform(length=1e-7, iq=0.1)
arb_wf = ArbitraryWaveform(amplitudes=np.linspace(0, 100))

Braket Pulse proporciona una biblioteca estándar de formas de onda, que incluye una forma de onda constante, una forma de onda gaussiana y una forma de onda de eliminación de derivadas mediante puerta adiabática (DRAG). Puede recuperar los datos de la forma de onda mediante la función sample para dibujar la forma de la onda, como se muestra en el siguiente ejemplo.

from braket.pulse import GaussianWaveform
import numpy as np
import matplotlib.pyplot as plt

zero_at_edge1 = GaussianWaveform(1e-7, 25e-9, 0.1, True)
# or zero_at_edge1 = GaussianWaveform(1e-7, 25e-9, 0.1)
zero_at_edge2 = GaussianWaveform(1e-7, 25e-9, 0.1, False)

times_1 = np.arange(0, zero_at_edge1.length, drive_frame.port.dt)
times_2 = np.arange(0, zero_at_edge2.length, drive_frame.port.dt)

plt.plot(times_1, zero_at_edge1.sample(drive_frame.port.dt))
plt.plot(times_2, zero_at_edge2.sample(drive_frame.port.dt))

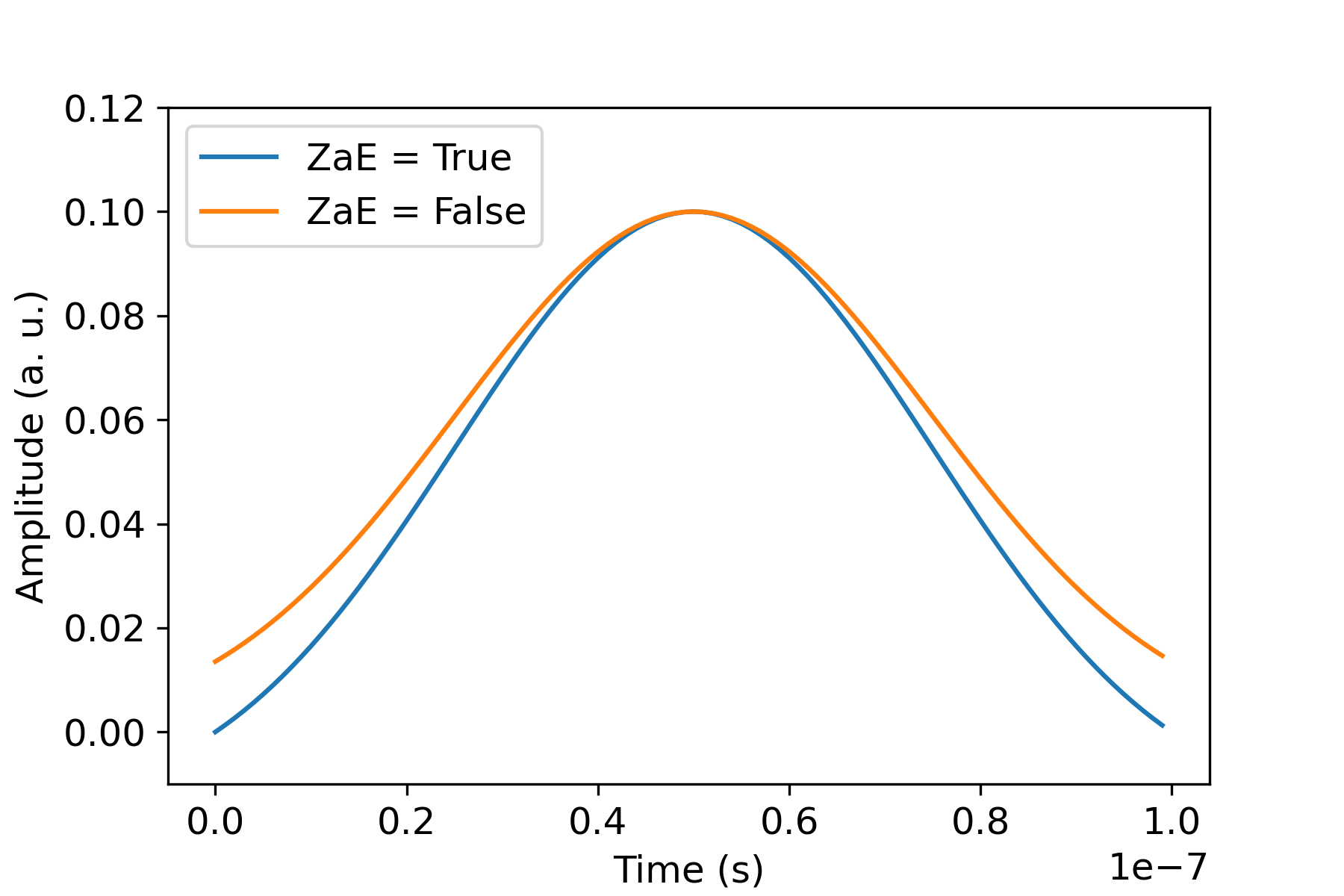
La imagen anterior muestra las formas de onda gaussianas creadas a partir de GaussianWaveform. Elegimos una longitud de pulso de 100 ns, una anchura de 25 ns y una amplitud de 0,1 (unidades arbitrarias). Las formas de onda se centran en la ventana de pulsos. GaussianWaveform acepta un argumento booleano zero_at_edges (ZaE en la leyenda). Cuando se establece en True, este argumento desplaza la forma de onda gaussiana de manera que los puntos en t=0 y t=length estén en cero y reescala la amplitud de manera que el valor máximo se corresponda con el argumento de amplitude.