Disponibilidade com redundância

Quando uma workload utiliza subsistemas múltiplos, independentes e redundantes, ela pode atingir um nível mais alto de disponibilidade teórica do que usando um único subsistema. Por exemplo, considere uma workload composta por dois subsistemas idênticos. Ele pode estar completamente operacional se o subsistema um ou o subsistema dois estiverem operacionais. Para que todo o sistema fique inativo, os dois subsistemas devem estar inativos ao mesmo tempo.

Se a probabilidade de falha de um subsistema for 1 − α, então a probabilidade de dois subsistemas redundantes estarem inativos ao mesmo tempo é o produto da probabilidade de falha de cada subsistema, F = (1−α₁) × (1−α₂). Para uma workload com dois subsistemas redundantes, usando a Equação (3), isso fornece uma disponibilidade definida como:

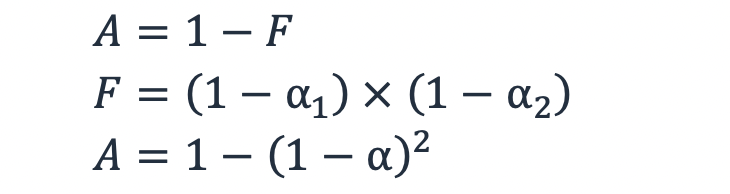
Equação 5

Portanto, para dois subsistemas cuja disponibilidade é de 99%, a probabilidade de um falhar é de 1% e a probabilidade de ambos falharem é (1−99%) × (1−99%) = 0,01%. Isso torna a disponibilidade usando dois subsistemas redundantes de 99,99%.

Isso também pode ser generalizado para incorporar peças de reposição redundantes adicionais s. Na Equação (5), assumimos apenas uma única peça de reposição, mas uma workload pode ter duas, três ou mais peças de reposição para que possa sobreviver à perda simultânea de vários subsistemas sem afetar a disponibilidade. Se uma workload tem três subsistemas e dois são de reposição, a probabilidade de que todos os três subsistemas falhem ao mesmo tempo é (1−α) × (1−α) × (1−α) or (1−α)³. Em geral, uma workload com s peças de reposição só falhará se os subsistemas s + 1 falharem.

Para uma workload com n subsistemas e s peças de reposição, f é o número de modos de falha ou as maneiras pelas quais os subsistemas s +1 podem falhar a partir de n.

Isso é efetivamente o teorema binomial, a matemática combinatória de escolher k elementos de um conjunto de n, ou “n escolher k”. Nesse caso, k é s + 1.

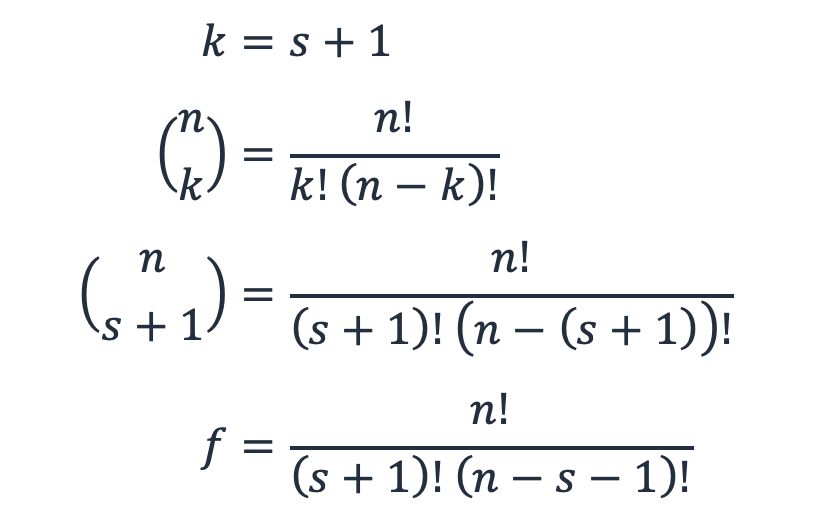
Equação 6

Podemos então produzir uma aproximação de disponibilidade generalizada que incorpora o número de modos de falha e a economia. (Para entender por que isso é uma aproximação, consulte o Apêndice 2 de Highleyman, et al. Quebrando a barreira da disponibilidade.)

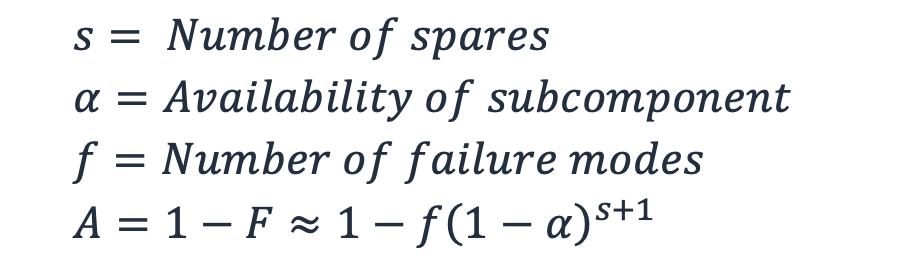
Equação 7

A economia pode ser aplicada a qualquer dependência que forneça recursos que falhem de forma independente. Instâncias do Amazon EC2 em diferentes AZs ou buckets do Amazon S3 em Regiões da AWS diferentes são exemplos disso. O uso de peças de reposição ajuda essa dependência a alcançar uma maior disponibilidade total para suportar as metas de disponibilidade da workload.

No entanto, economizar tem um custo. Cada reposição adicional custa o mesmo que o módulo original, aumentando o custo pelo menos linearmente. Criar uma workload que possa usar peças de reposição também aumenta sua complexidade. Ele deve saber como identificar falhas de dependência, transformar o trabalho em um recurso saudável e gerenciar a capacidade geral da workload.

A redundância é um problema de otimização. Poucas peças de reposição e a workload pode falhar com mais frequência do que o desejado, muitas peças sobressalentes e a workload custa muito para ser executada. Há um limite no qual adicionar mais peças de reposição custará mais do que a disponibilidade adicional que elas obtêm garante.

Usando nossa fórmula de disponibilidade geral com peças de reposição, Equação (7), para um subsistema que tem uma disponibilidade de 99,5%, com duas peças de reposição, a disponibilidade da workload é A ≈ 1 − (1) (1−0,95) ³ = 99,9999875% (aproximadamente 3,94 segundos de tempo de inatividade por ano), e com 10 peças de reposição, obtemos A ≈ 1 − (1) (1−0,995) ¹¹ = 25,5 9^′s (o tempo de inatividade aproximado seria 1,26252 × 10 ⁻¹⁵ms por ano, efetivamente 0). Ao comparar essas duas workloads, incorremos em um aumento de 5 vezes no custo de economia para obter quatro segundos a menos de tempo de inatividade por ano. Para a maioria das workloads, o aumento no custo seria injustificado devido a esse aumento na disponibilidade. A figura a seguir mostra essa relação.

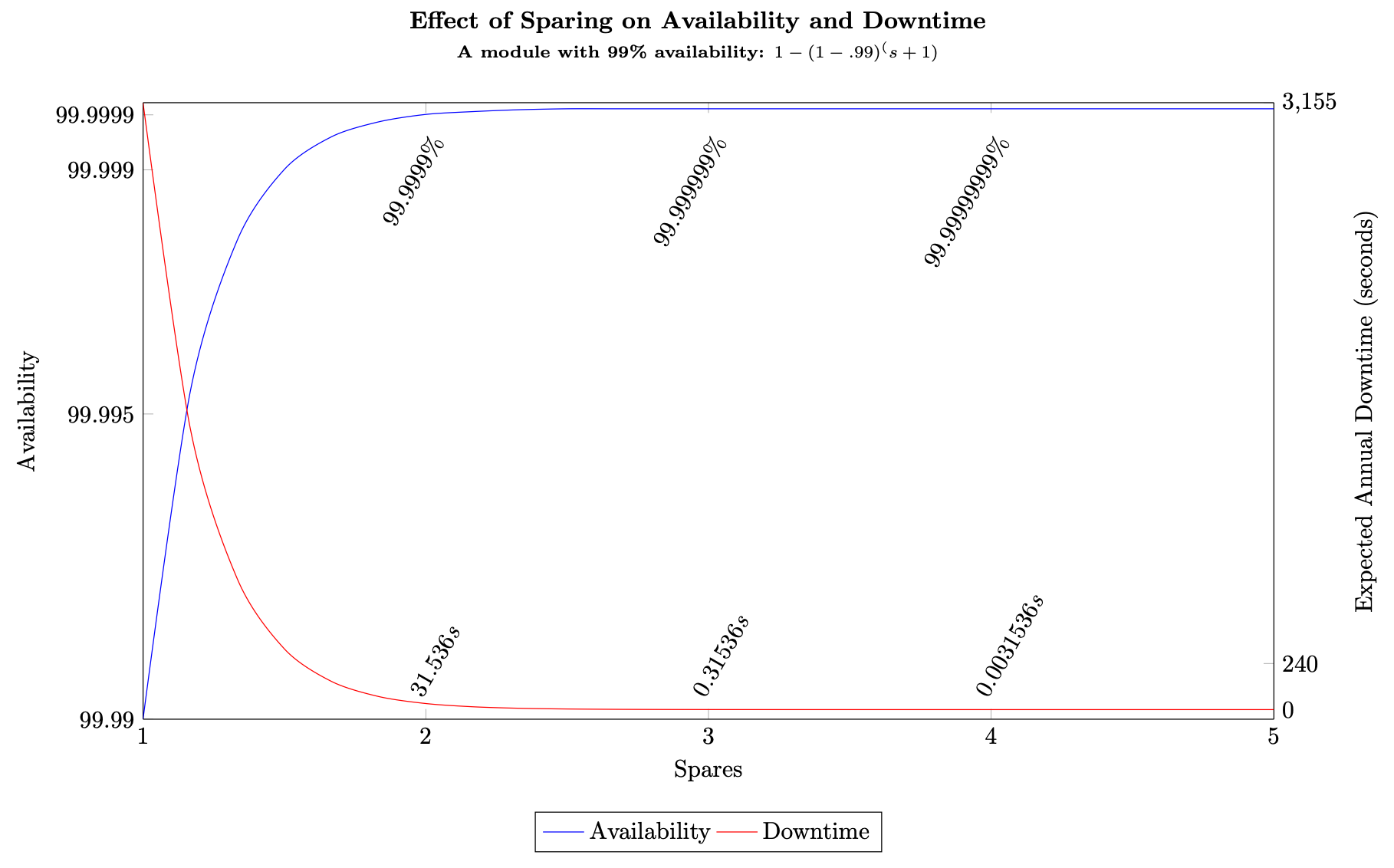
Retornos decrescentes decorrentes do aumento da poupança

Com três peças de reposição ou mais, o resultado são frações de segundo do tempo de inatividade esperado por ano, o que significa que, após esse ponto, você atinge a área de retornos decrescentes. Pode haver uma necessidade de “adicionar mais” para alcançar níveis mais altos de disponibilidade, mas, na realidade, o custo-benefício desaparece muito rapidamente. O uso de mais de três peças de reposição não fornece um ganho material perceptível para quase todas as workloads quando o próprio subsistema tem pelo menos 99% de disponibilidade.

Você deve considerar a unidade de falha ao selecionar o número correto de peças de reposição. Por exemplo, vamos examinar uma workload que requer 10 instâncias do EC2 para lidar com a capacidade de pico e elas são implantadas em uma única AZ.

Como as AZs foram projetadas para serem limites de isolamento de falhas, a unidade de falha não é apenas uma única instância do EC2, porque uma AZ inteira de instâncias do EC2 pode falhar em conjunto. Nesse caso, você desejará adicionar redundância com outra AZ, implantando 10 instâncias EC2 adicionais para lidar com a carga em caso de falha de AZ, totalizando 20 instâncias EC2 (seguindo o padrão de estabilidade estática).

Embora pareçam ser 10 instâncias extras do EC2, na verdade é apenas uma única AZ sobressalente, portanto, não excedemos o ponto de retornos decrescentes. No entanto, você pode ser ainda mais econômico e, ao mesmo tempo, aumentar sua disponibilidade utilizando três AZs e implantando cinco instâncias EC2 por AZ.

Isso fornece uma AZ extra com um total de 15 instâncias EC2 (versus duas AZs com 20 instâncias), ainda fornecendo o total de 10 instâncias necessárias para atender à capacidade máxima durante um evento que afeta uma única AZ. Portanto, você deve incorporar o sparing para ser tolerante a falhas em todos os limites de isolamento de falhas usados pela workload (instância, célula, AZ e região).