As traduções são geradas por tradução automática. Em caso de conflito entre o conteúdo da tradução e da versão original em inglês, a versão em inglês prevalecerá.

Olá AHS: Execute sua primeira simulação hamiltoniana analógica

Esta seção fornece informações sobre como executar sua primeira simulação hamiltoniana analógica.

Cadeia de rotação interativa

Para um exemplo canônico de um sistema de muitas partículas interagindo, vamos considerar um anel de oito giros (cada um dos quais pode estar nos estados “para cima” ⟩ e “para baixo” ↓⟩). Embora pequeno, esse sistema modelo já exibe um punhado de fenômenos interessantes de materiais magnéticos que ocorrem naturalmente. Neste exemplo, mostraremos como preparar a chamada ordem antiferromagnética, em que giros consecutivos apontam em direções opostas.

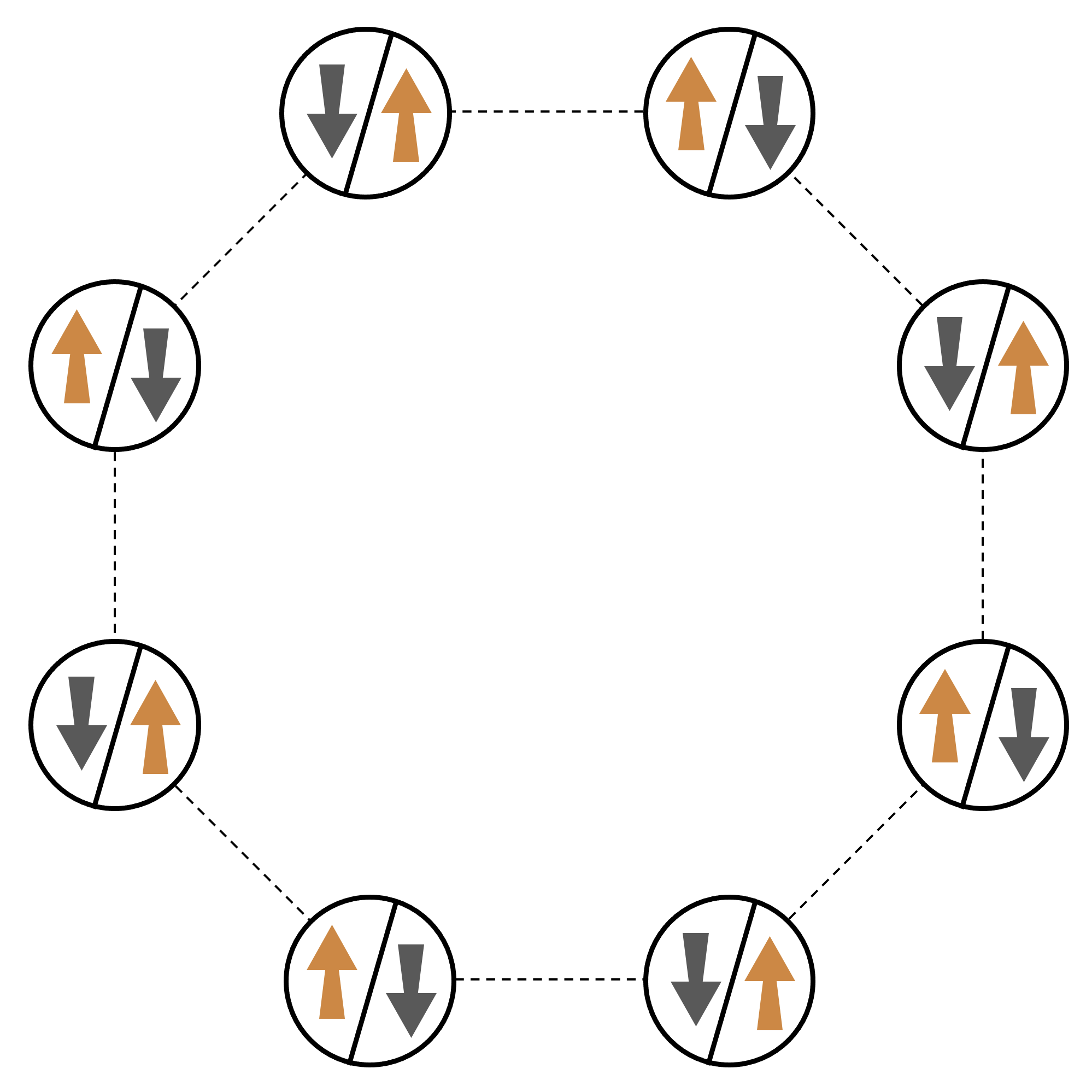
Arranjo

Usaremos um átomo neutro para representar cada spin, e os estados de spin “para cima” e “para baixo” serão codificados no estado excitado de Rydberg e no estado fundamental dos átomos, respectivamente. Primeiro, criaremos o arranjo 2-d. Podemos programar o anel de giros acima com o código a seguir.

Pré-requisitos: Você precisa instalar pip o SDK do Braket. (Se você estiver usando uma instância de caderno hospedada no Braket, esse SDK vem pré-instalado com os cadernos.) Para reproduzir os gráficos, você também precisa instalar separadamente o matplotlib com o comando shell pip install matplotlib.

from braket.ahs.atom_arrangement import AtomArrangement
import numpy as np
import matplotlib.pyplot as plt  # Required for plotting

a = 5.7e-6  # Nearest-neighbor separation (in meters)

register = AtomArrangement()
register.add(np.array([0.5, 0.5 + 1/np.sqrt(2)]) * a)
register.add(np.array([0.5 + 1/np.sqrt(2), 0.5]) * a)
register.add(np.array([0.5 + 1/np.sqrt(2), - 0.5]) * a)
register.add(np.array([0.5, - 0.5 - 1/np.sqrt(2)]) * a)
register.add(np.array([-0.5, - 0.5 - 1/np.sqrt(2)]) * a)
register.add(np.array([-0.5 - 1/np.sqrt(2), - 0.5]) * a)
register.add(np.array([-0.5 - 1/np.sqrt(2), 0.5]) * a)
register.add(np.array([-0.5, 0.5 + 1/np.sqrt(2)]) * a)

com o qual também podemos traçar

fig, ax = plt.subplots(1, 1, figsize=(7, 7))
xs, ys = [register.coordinate_list(dim) for dim in (0, 1)]
ax.plot(xs, ys, 'r.', ms=15)

for idx, (x, y) in enumerate(zip(xs, ys)):
    ax.text(x, y, f" {idx}", fontsize=12)

plt.show()  # This will show the plot below in an ipython or jupyter session

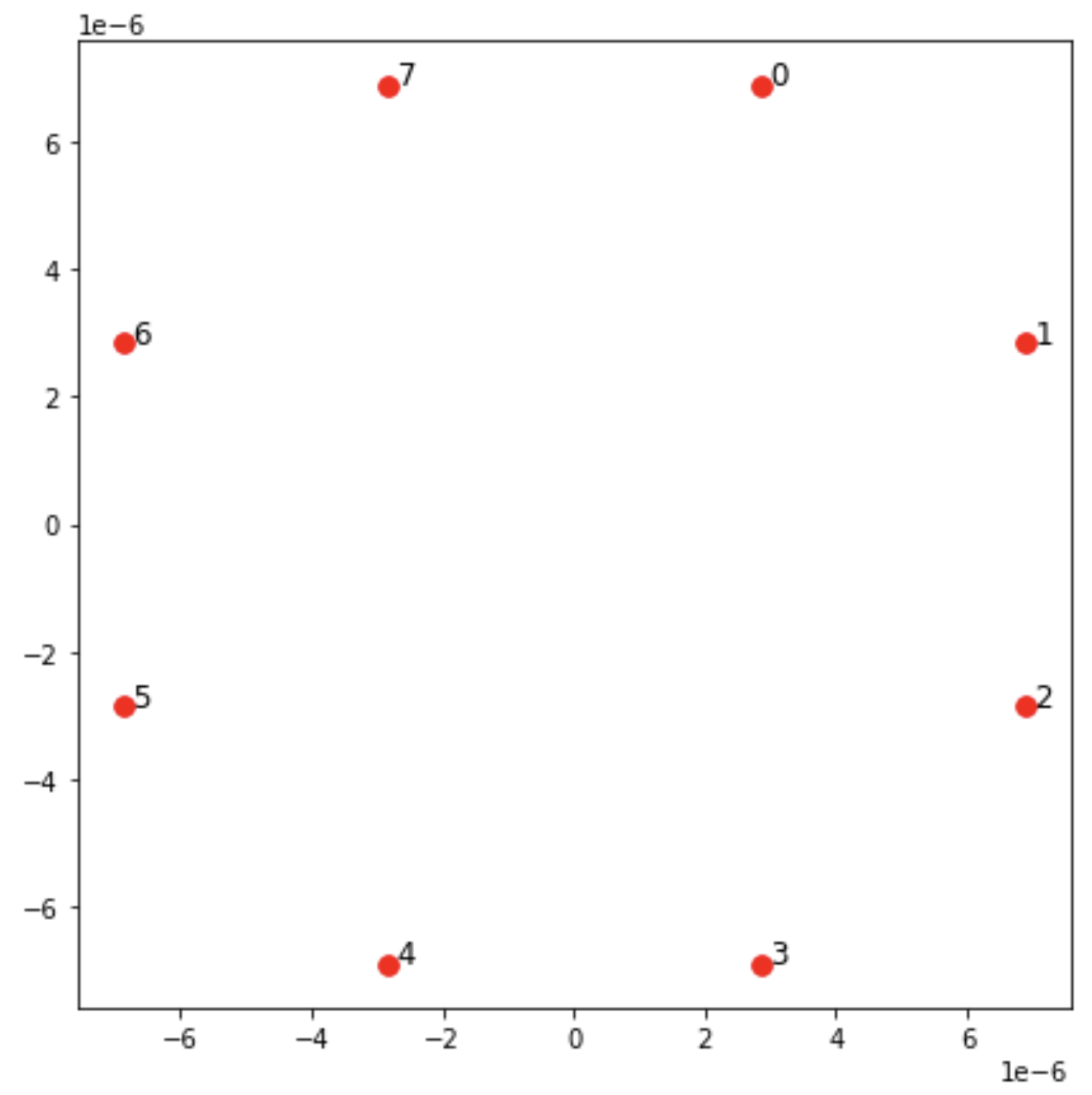
Interação

Para preparar a fase antiferromagnética, precisamos induzir interações entre spins vizinhos. Usamos a interação van der Waals para isso, que é implementada nativamente por dispositivos de átomos neutros (como o dispositivo Aquila de QuEra). Usando a representação de spin, o termo hamiltoniano para essa interação pode ser expresso como uma soma de todos os pares de spin (j, k).

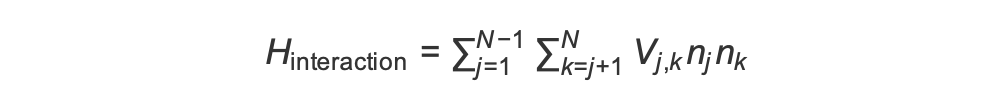
Aqui, nj=↑ _j ⟨↑ _j é um operador que assume o valor de 1 somente se o spin j estiver no estado “ativo” e 0 caso contrário. A força é V _j,k =C₆/(d_j,k​) ⁶, onde C ₆ é o coeficiente fixo e d _j,k é a distância euclidiana entre os spins j e k. O efeito imediato desse termo de interação é que qualquer estado em que o spin j e o spin k estejam “para cima” tem energia elevada (na quantidade V_j,k). Ao projetar cuidadosamente o resto do programa AHS, essa interação evitará que ambas as rodadas vizinhas fiquem no estado “ativo”, um efeito comumente conhecido como “bloqueio de Rydberg”.

Campo de condução

No início do programa AHS, todos os giros (por padrão) começam em seu estado “inativo”, eles estão na chamada fase ferromagnética. De olho em nosso objetivo de preparar a fase antiferromagnética, especificamos um campo de condução coerente dependente do tempo que faz a transição suave dos giros desse estado para um estado de muitos corpos, onde os estados “ascendentes” são preferidos. O hamiltoniano correspondente pode ser escrito como

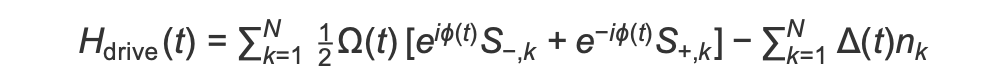
onde Ω (t), θ (t), Δ (t) são a amplitude global dependente do tempo (também conhecida como frequência Rabi), a fase e o desajuste do campo de direção, afetando todos os giros de maneira uniforme. Aqui, S_−,k​=∣↓_k​⟩⟨↑_k​∣e S_+,k​​=(S_−,k​)^†=∣↑_k​⟩⟨↓_k​∣ são os operadores de abaixamento e elevação do spin k, respectivamente, e n_k​=∣↑_k​⟩⟨↑_k​∣é o mesmo operador de antes. A parte Ω do campo de condução acopla coerentemente os estados “para baixo” e “para cima” de todos os giros simultaneamente, enquanto a parte Δ controla a recompensa de energia para os estados “para cima”.

Para programar uma transição suave da fase ferromagnética para a fase antiferromagnética, especificamos o campo de condução com o código a seguir.

from braket.timings.time_series import TimeSeries
from braket.ahs.driving_field import DrivingField

# Smooth transition from "down" to "up" state
time_max = 4e-6  # seconds
time_ramp = 1e-7  # seconds
omega_max = 6300000.0  # rad / sec
delta_start = -5 * omega_max
delta_end = 5 * omega_max

omega = TimeSeries()
omega.put(0.0, 0.0)
omega.put(time_ramp, omega_max)
omega.put(time_max - time_ramp, omega_max)
omega.put(time_max, 0.0)

delta = TimeSeries()
delta.put(0.0, delta_start)
delta.put(time_ramp, delta_start)
delta.put(time_max - time_ramp, delta_end)
delta.put(time_max, delta_end)

phi = TimeSeries().put(0.0, 0.0).put(time_max, 0.0)

drive = DrivingField(
   amplitude=omega,
   phase=phi,
   detuning=delta
)

Podemos visualizar a série temporal do campo de condução com o seguinte script.

fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)

ax = axes[0]
time_series = drive.amplitude.time_series
ax.plot(time_series.times(), time_series.values(), '.-')
ax.grid()
ax.set_ylabel('Omega [rad/s]')

ax = axes[1]
time_series = drive.detuning.time_series
ax.plot(time_series.times(), time_series.values(), '.-')
ax.grid()
ax.set_ylabel('Delta [rad/s]')

ax = axes[2]
time_series = drive.phase.time_series
# Note: time series of phase is understood as a piecewise constant function
ax.step(time_series.times(), time_series.values(), '.-', where='post')
ax.set_ylabel('phi [rad]')
ax.grid()
ax.set_xlabel('time [s]')

plt.show()  # This will show the plot below in an ipython or jupyter session

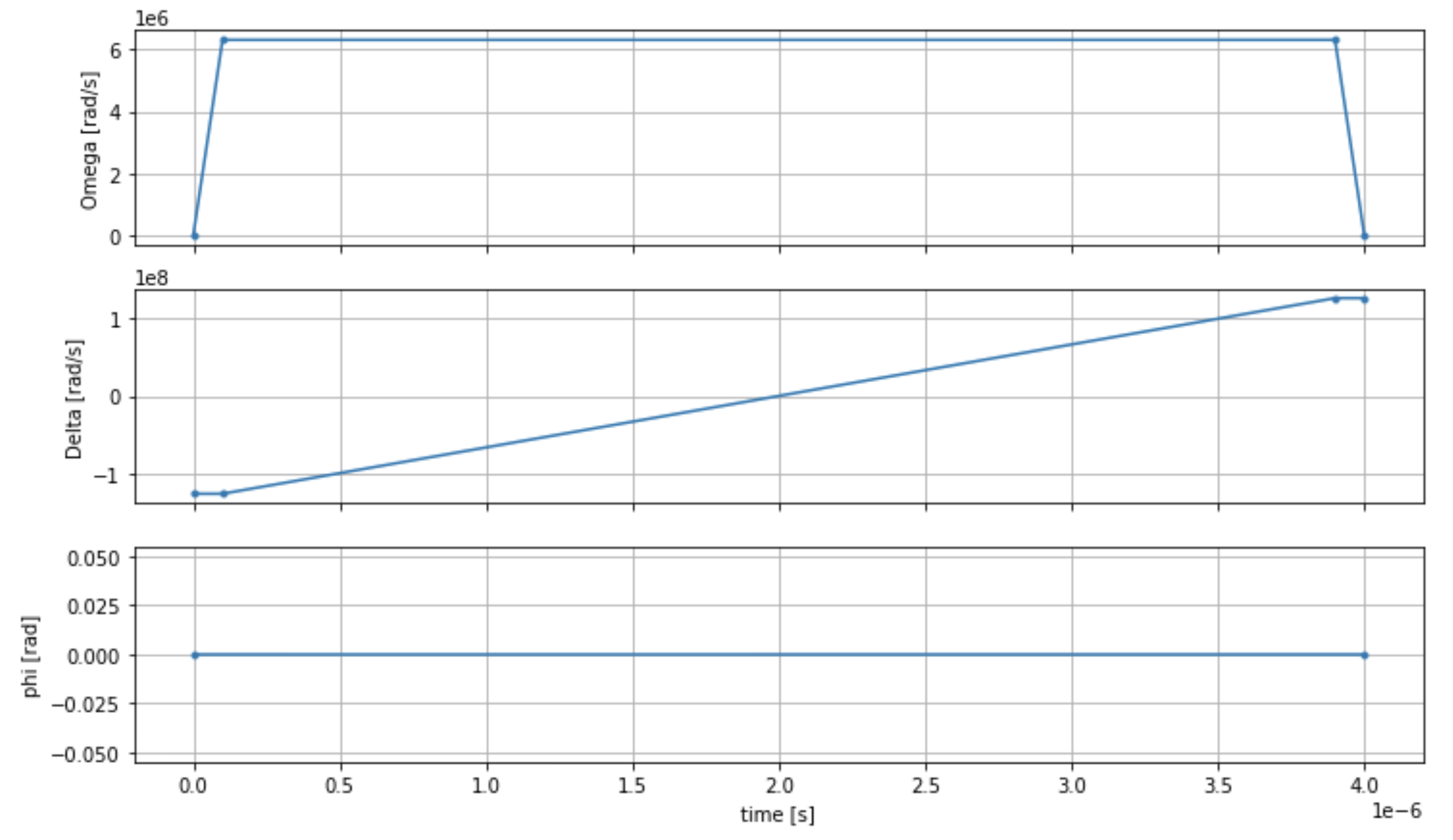
Programa AHS

O registro, o campo motriz (e as interações implícitas de van der Waals) compõem o programa de simulação hamiltoniana analógica ahs_program.

from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation

ahs_program = AnalogHamiltonianSimulation(
   register=register,
   hamiltonian=drive
)

Executando no simulador local

Como esse exemplo é pequeno (menos de 15 rodadas), antes de executá-lo em uma QPU compatível com AHS, podemos executá-lo no simulador AHS local que vem com o SDK Braket. Como o simulador local está disponível gratuitamente com o SDK do Braket, essa é a melhor prática para garantir que nosso código possa ser executado corretamente.

Aqui, podemos definir o número de fotos para um valor alto (digamos, 1 milhão) porque o simulador local rastreia a evolução temporal do estado quântico e extrai amostras do estado final; portanto, aumenta o número de fotos e aumenta o runtime total apenas marginalmente.

from braket.devices import LocalSimulator

device = LocalSimulator("braket_ahs")

result_simulator = device.run(
   ahs_program,
   shots=1_000_000
).result()  # Takes about 5 seconds

Analisar resultados de simulação

Podemos agregar os resultados da captura com a seguinte função que infere o estado de cada rotação (que pode ser “d” para “para baixo”, “u” para “para cima” ou “e” para local vazio) e conta quantas vezes cada configuração ocorreu nas fotos.

from collections import Counter


def get_counts(result):
    """Aggregate state counts from AHS shot results

    A count of strings (of length = # of spins) are returned, where
    each character denotes the state of a spin (site):
      e: empty site
      u: up state spin
      d: down state spin

    Args:
      result (braket.tasks.analog_hamiltonian_simulation_quantum_task_result.AnalogHamiltonianSimulationQuantumTaskResult)

    Returns
       dict: number of times each state configuration is measured

    """
    state_counts = Counter()
    states = ['e', 'u', 'd']
    for shot in result.measurements:
        pre = shot.pre_sequence
        post = shot.post_sequence
        state_idx = np.array(pre) * (1 + np.array(post))
        state = "".join(map(lambda s_idx: states[s_idx], state_idx))
        state_counts.update((state,))
    return dict(state_counts)


counts_simulator = get_counts(result_simulator)  # Takes about 5 seconds
print(counts_simulator)

*[Output]*
{'dddddddd': 5, 'dddddddu': 12, 'ddddddud': 15, ...}

Aqui counts está um dicionário que conta o número de vezes que cada configuração de estado é observada nas fotos. Também podemos visualizá-los com o código a seguir.

from collections import Counter


def has_neighboring_up_states(state):
    if 'uu' in state:
        return True
    if state[0] == 'u' and state[-1] == 'u':
        return True
    return False


def number_of_up_states(state):
    return Counter(state)['u']


def plot_counts(counts):
    non_blockaded = []
    blockaded = []
    for state, count in counts.items():
        if not has_neighboring_up_states(state):
            collection = non_blockaded
        else:
            collection = blockaded
        collection.append((state, count, number_of_up_states(state)))

    blockaded.sort(key=lambda _: _[1], reverse=True)
    non_blockaded.sort(key=lambda _: _[1], reverse=True)

    for configurations, name in zip((non_blockaded,
                                     blockaded),
                                    ('no neighboring "up" states',
                                     'some neighboring "up" states')):
        plt.figure(figsize=(14, 3))
        plt.bar(range(len(configurations)), [item[1] for item in configurations])
        plt.xticks(range(len(configurations)))
        plt.gca().set_xticklabels([item[0] for item in configurations], rotation=90)
        plt.ylabel('shots')
        plt.grid(axis='y')
        plt.title(f'{name} configurations')
        plt.show()


plot_counts(counts_simulator)

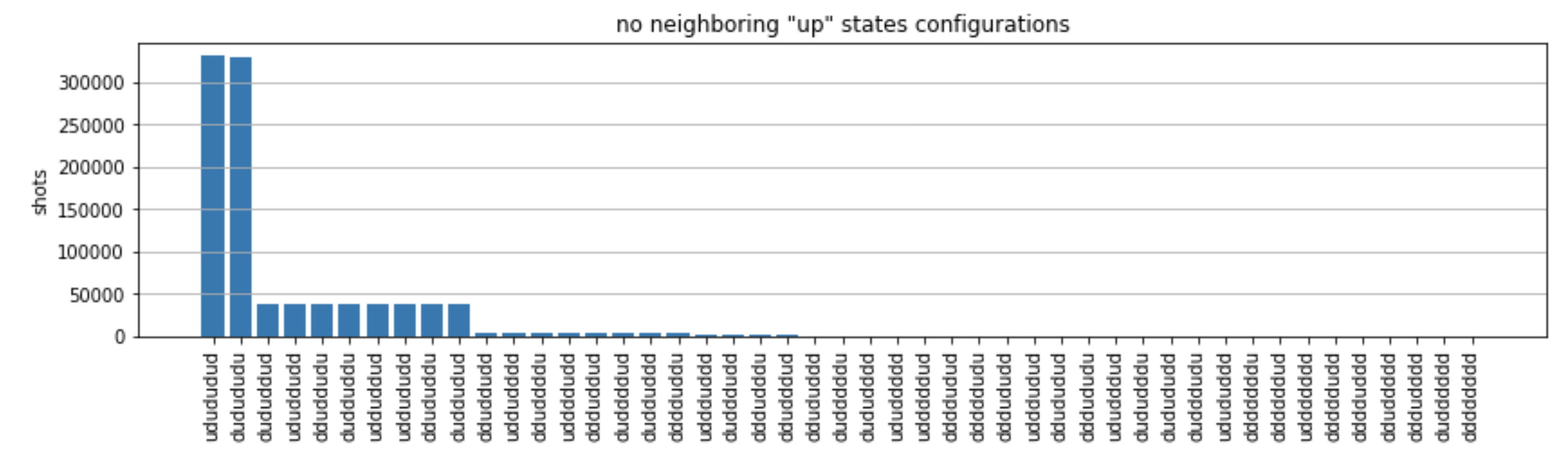
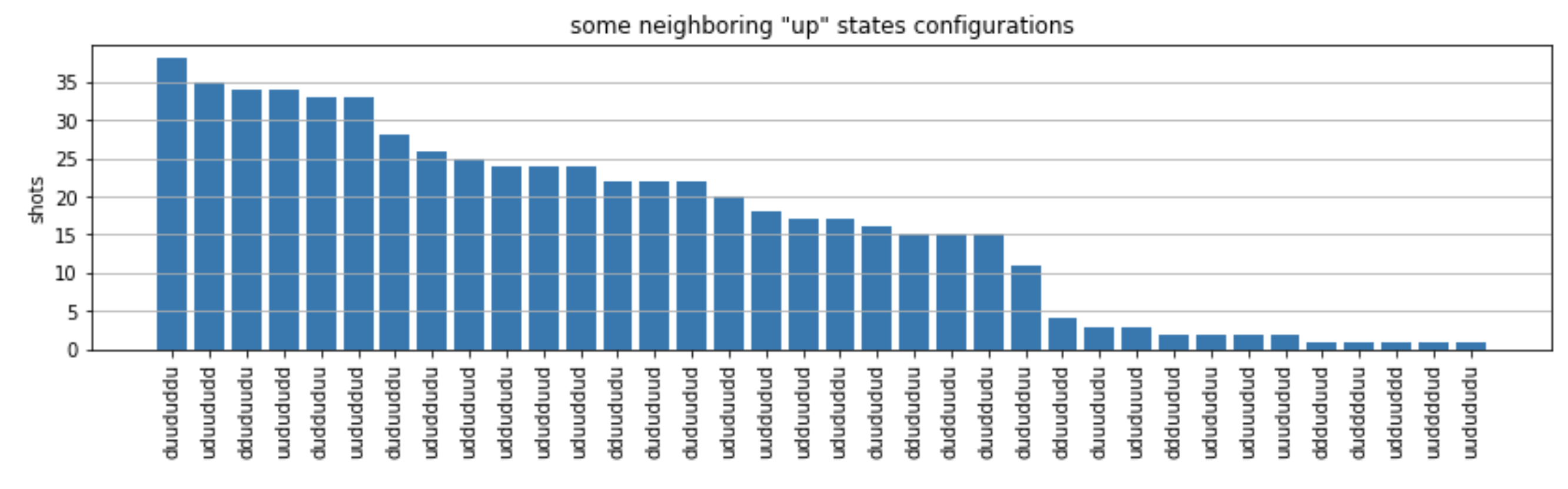
A partir dos gráficos, podemos ler as seguintes observações para verificar se preparamos com sucesso a fase antiferromagnética.

Executando no QuEra Aquila QPU

Pré-requisitos: Além da instalação rápida do SDK do Braket, se você for novo no Amazon Braket, certifique-se de ter concluído as etapas necessárias do Passos para começar.

Com todas as dependências instaladas, podemos nos conectar à QPU Aquila.

from braket.aws import AwsDevice

aquila_qpu = AwsDevice("arn:aws:braket:us-east-1::device/qpu/quera/Aquila")

Para tornar nosso programa AHS adequado para a máquina QuEra, precisamos arredondar todos os valores para cumprir os níveis de precisão permitidos pela QPU Aquila. Esses requisitos são regidos pelos parâmetros do dispositivo com “Resolução” no nome. Podemos vê-los executando aquila_qpu.properties.dict() em um caderno. Para obter mais detalhes sobre os recursos e requisitos do Aquila, consulte a Introdução ao caderno Aquila. Podemos fazer isso chamando o método discretize.

discretized_ahs_program = ahs_program.discretize(aquila_qpu)

Agora podemos executar o programa (executando apenas 100 fotos por enquanto) na QPU Aquila.

task = aquila_qpu.run(discretized_ahs_program, shots=100)

metadata = task.metadata()
task_arn = metadata['quantumTaskArn']
task_status = metadata['status']

print(f"ARN: {task_arn}")
print(f"status: {task_status}")

*[Output]*
ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
status: CREATED

Devido à grande variação de quanto tempo uma tarefa quântica pode levar para ser executada (dependendo das janelas de disponibilidade e da utilização da QPU), é uma boa ideia anotar o ARN da tarefa quântica, para que possamos verificar seu status posteriormente com o seguinte trecho de código.

# Optionally, in a new python session
from braket.aws import AwsQuantumTask

SAVED_TASK_ARN = "arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef"

task = AwsQuantumTask(arn=SAVED_TASK_ARN)
metadata = task.metadata()
task_arn = metadata['quantumTaskArn']
task_status = metadata['status']

print(f"ARN: {task_arn}")
print(f"status: {task_status}")

*[Output]*
ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
status: COMPLETED

Depois que o status for CONCLUÍDO (o que também pode ser verificado na página de tarefas quânticas do console Amazon Braket), podemos consultar os resultados com:

result_aquila = task.result()

Analisando os resultados da QPU

Usando as mesmas funções get_counts de antes, podemos calcular as contagens:

counts_aquila = get_counts(result_aquila)
   print(counts_aquila)

*[Output]*
{'dddududd': 2, 'dudududu': 18, 'ddududud': 4, ...}

e plote-os com plot_counts:

plot_counts(counts_aquila)

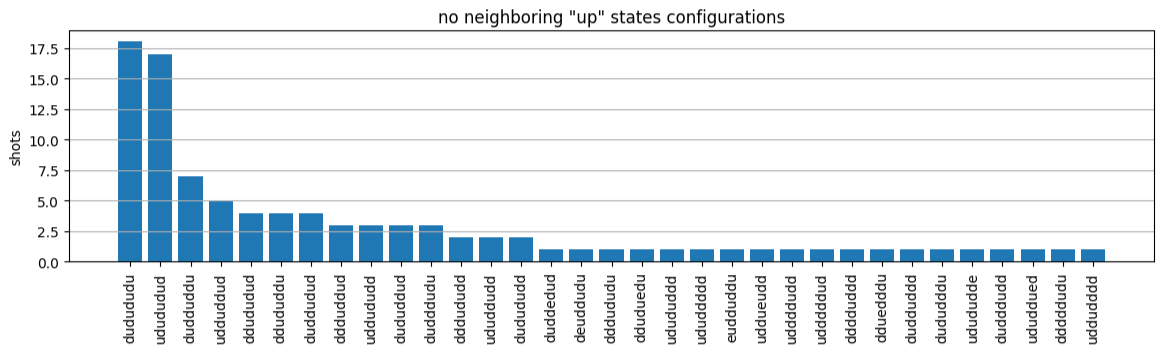
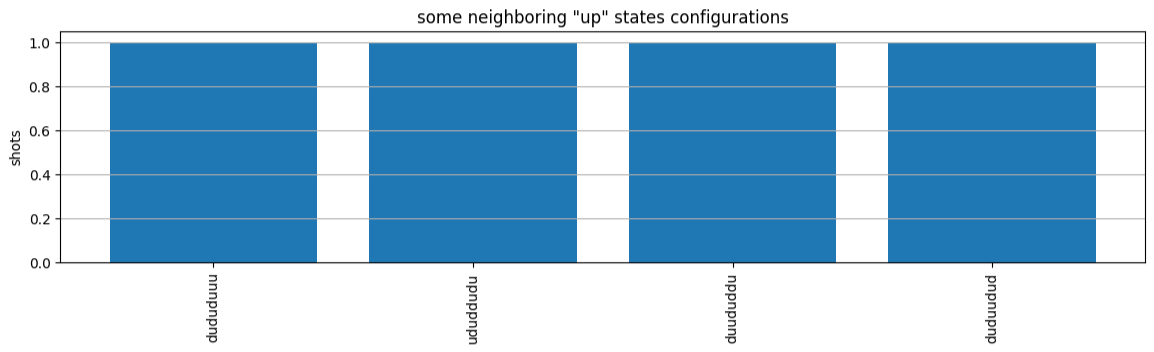
Observe que uma pequena fração das fotos tem locais vazios (marcados com “e”). Isso se deve a imperfeições de 1 a 2% por átomo na preparação do QPU Aquila. Além disso, os resultados coincidem com a simulação dentro da flutuação estatística esperada devido ao pequeno número de disparos.

Próximas etapas

Parabéns, agora você executou sua primeira workload de AHS no Amazon Braket usando o simulador AHS local e a QPU Aquila.

Para saber mais sobre a física de Rydberg, a simulação hamiltoniana analógica e o dispositivo Aquila, consulte nossos exemplos de cadernos.