상호 작용 스핀 체인 배열 상호 작용 구동장 AHS 프로그램 로컬 시뮬레이터에서 실행 시뮬레이터 결과 분석 QuEra의 Aquila QPU에서 실행 QPU 결과 분석 다음 단계

Hello AHS: 첫 번째 아날로그 해밀토니안 시뮬레이션 실행

이 섹션에서는 첫 번째 아날로그 해밀토니안 시뮬레이션을 실행하는 방법에 대한 정보를 제공합니다.

이 섹션의 내용:

상호 작용 스핀 체인
배열
상호 작용
구동장
AHS 프로그램
로컬 시뮬레이터에서 실행
시뮬레이터 결과 분석
QuEra의 Aquila QPU에서 실행
QPU 결과 분석
다음 단계

상호 작용 스핀 체인

상호 작용하는 입자가 많은 시스템의 표준 예제로, 8개의 스핀으로 이루어진 고리를 생각해 보겠습니다(각각 “up” ∣↑⟩ 및 “down” ∣↓⟩ 상태일 수 있음). 이 모델 시스템은 비록 작지만, 이미 자연적으로 발생하는 자성 물질의 몇 가지 흥미로운 현상을 보여줍니다. 이 예제에서는 연속적인 스핀이 반대 방향을 가리키는 소위 반강자성 정렬을 준비하는 방법을 보여줍니다.

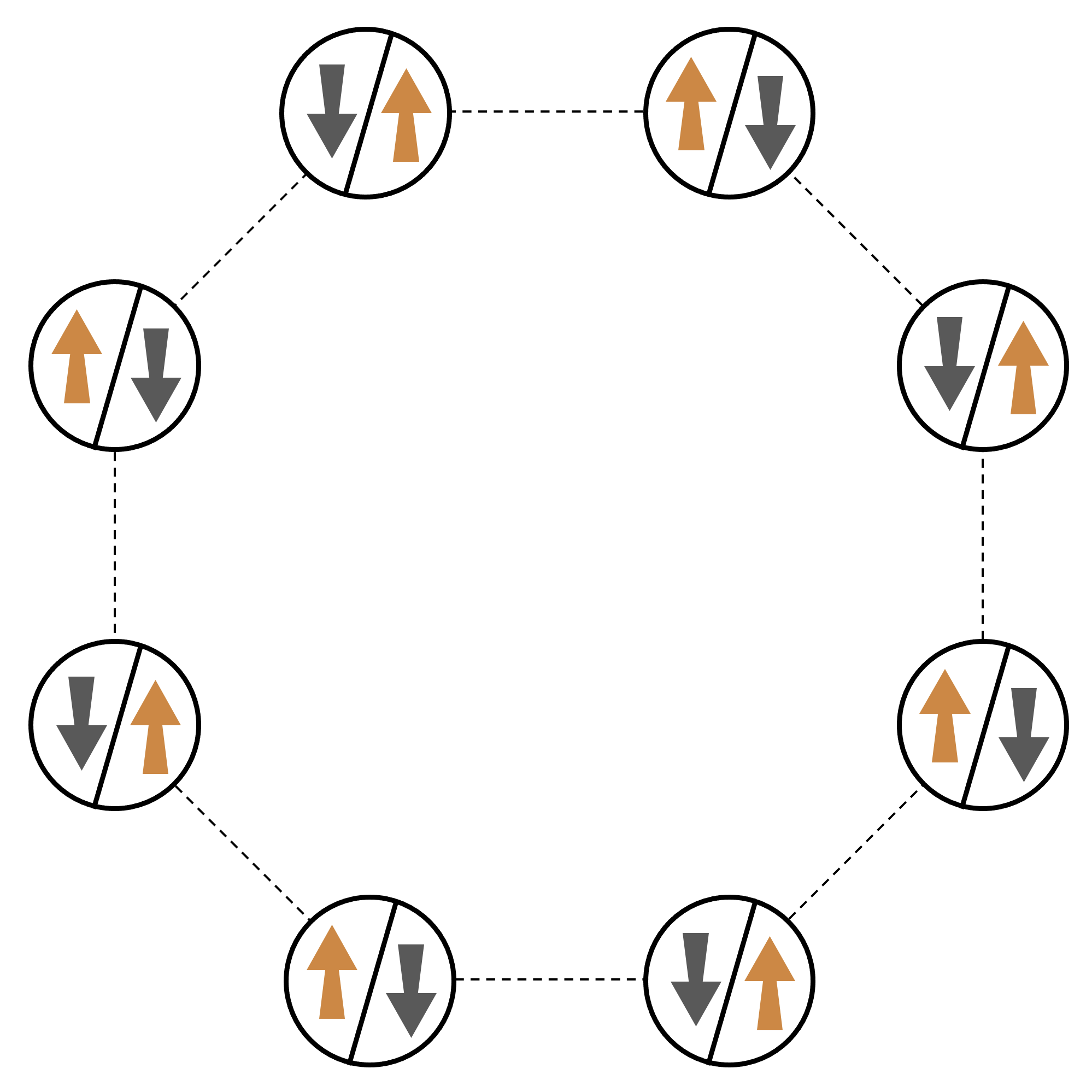
위쪽 및 아래쪽 반전 화살표가 포함된 8개의 원 노드를 연결하는 다이어그램입니다.

배열

각 스핀을 나타내기 위해 하나의 중성 원자를 사용하며, “up” 및 “down” 스핀 상태는 각각 원자의 여기된 Rydberg 상태와 바닥 상태로 인코딩됩니다. 먼저 2차원 배열을 생성합니다. 다음 코드를 사용하여 위의 스핀 고리를 프로그래밍할 수 있습니다.

사전 조건: Braket SDK를 pip 설치해야 합니다. (Braket 호스팅 노트북 인스턴스를 사용하는 경우 이 SDK는 노트북과 함께 사전 설치되어 제공됩니다.) 플롯을 재현하려면 shell 명령 pip install matplotlib을 사용하여 matplotlib을 별도로 설치해야 합니다.


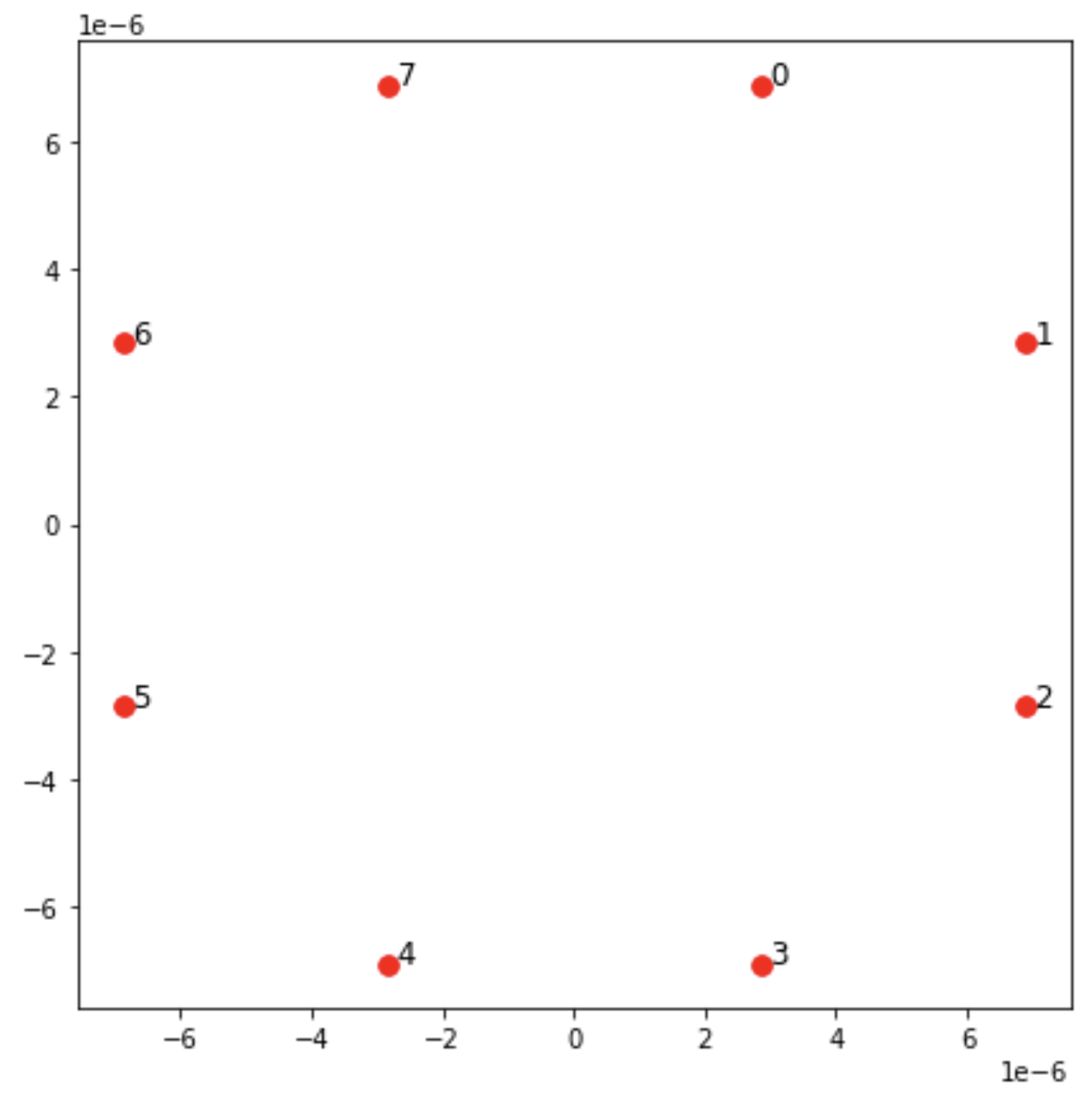
from braket.ahs.atom_arrangement import AtomArrangement
import numpy as np
import matplotlib.pyplot as plt  # Required for plotting

a = 5.7e-6  # Nearest-neighbor separation (in meters)

register = AtomArrangement()
register.add(np.array([0.5, 0.5 + 1/np.sqrt(2)]) * a)
register.add(np.array([0.5 + 1/np.sqrt(2), 0.5]) * a)
register.add(np.array([0.5 + 1/np.sqrt(2), - 0.5]) * a)
register.add(np.array([0.5, - 0.5 - 1/np.sqrt(2)]) * a)
register.add(np.array([-0.5, - 0.5 - 1/np.sqrt(2)]) * a)
register.add(np.array([-0.5 - 1/np.sqrt(2), - 0.5]) * a)
register.add(np.array([-0.5 - 1/np.sqrt(2), 0.5]) * a)
register.add(np.array([-0.5, 0.5 + 1/np.sqrt(2)]) * a)

또한 다음으로 플롯할 수 있습니다.


fig, ax = plt.subplots(1, 1, figsize=(7, 7))
xs, ys = [register.coordinate_list(dim) for dim in (0, 1)]
ax.plot(xs, ys, 'r.', ms=15)

for idx, (x, y) in enumerate(zip(xs, ys)):
    ax.text(x, y, f" {idx}", fontsize=12)

plt.show()  # This will show the plot below in an ipython or jupyter session

두 축의 양수 값과 음수 값에 걸쳐 분포된 점을 보여주는 산점도 플롯입니다.

상호 작용

반강자성 위상을 준비하려면 이웃하는 스핀 간의 상호 작용을 유도해야 합니다. 이를 위해 van der Waals 상호 작용을 사용합니다. 이 상호 작용은 기본적으로 중성 원자 디바이스(예: QuEra의 Aquila 디바이스)에 의해 구현됩니다. 스핀 표현을 사용하면 이 상호 작용에 대한 해밀토니안 항을 모든 스핀 쌍(j,k)에 대한 합으로 표현할 수 있습니다.

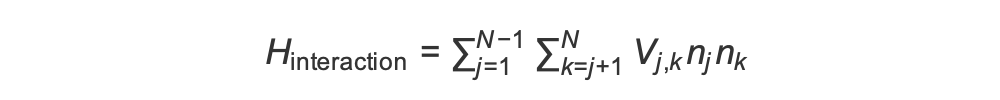
여기서 nj=∣↑_j⟩⟨↑_j∣는 스핀 j가 “up” 상태에 있는 경우에만 1, 그렇지 않으면 0의 값을 취하는 연산자입니다. 강도는 V_j,k=C₆/(d_j,k)⁶이며, 여기서 C₆은 고정 계수이고 d_j,k는 스핀 j와 k 사이의 유클리드 거리입니다. 이 상호 작용 항의 즉각적인 효과는 스핀 j와 스핀 k가 “up”인 모든 상태의 에너지가 (V_j,k 만큼) 증가한다는 것입니다. AHS 프로그램의 나머지 부분을 신중하게 설계함으로써, 이 상호 작용은 이웃한 스핀이 모두 “up” 상태에 있는 것을 방지합니다. 이는 일반적으로 "Rydberg 봉쇄"로 알려진 효과입니다.

구동장

AHS 프로그램을 시작할 때 모든 스핀은 (기본적으로) “down” 상태에서 시작되며 소위 강자성 위상에 있습니다. 반강자성 위상을 준비한다는 목표를 염두에 두고, 이 상태에서 "up" 상태가 선호되는 다체 상태로 스핀을 원활하게 전환하는 시간 종속 결맞음 구동장을 지정합니다. 해당 해밀토니안은 다음과 같이 쓸 수 있습니다.

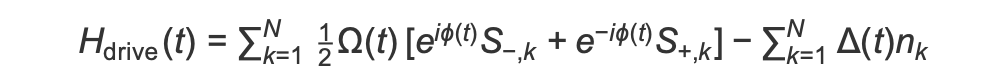
여기서 Ω(t),ϕ(t),Δ(t)는 모든 스핀에 균일하게 영향을 미치는 구동장의 시간 종속 전역 진폭(Rabi 주파수라고도 함), 위상 및 디튜닝입니다. 여기서 S_−,k=∣↓_k⟩⟨↑_k∣and S_+,k=(S_−,k)^†=∣↑_k⟩⟨↓_k∣은 각각 스핀 k의 하강 및 상승 연산자이고, n_k=∣↑_k⟩⟨↑_k∣는 이전과 동일한 연산자입니다. 구동장의 Ω 부분은 모든 스핀의 "down" 상태와 "up" 상태를 동시에 일관되게 결합하고 Δ 부분은 "up" 상태에 대한 에너지 보상을 제어합니다.

강자성 위상에서 반강자성 위상으로의 원활한 전환을 프로그래밍하기 위해 다음 코드로 구동장을 지정합니다.


from braket.timings.time_series import TimeSeries
from braket.ahs.driving_field import DrivingField

# Smooth transition from "down" to "up" state
time_max = 4e-6  # seconds
time_ramp = 1e-7  # seconds
omega_max = 6300000.0  # rad / sec
delta_start = -5 * omega_max
delta_end = 5 * omega_max

omega = TimeSeries()
omega.put(0.0, 0.0)
omega.put(time_ramp, omega_max)
omega.put(time_max - time_ramp, omega_max)
omega.put(time_max, 0.0)

delta = TimeSeries()
delta.put(0.0, delta_start)
delta.put(time_ramp, delta_start)
delta.put(time_max - time_ramp, delta_end)
delta.put(time_max, delta_end)

phi = TimeSeries().put(0.0, 0.0).put(time_max, 0.0)

drive = DrivingField(
   amplitude=omega,
   phase=phi,
   detuning=delta
)

다음 스크립트를 사용하여 구동장의 시계열을 시각화할 수 있습니다.


fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)

ax = axes[0]
time_series = drive.amplitude.time_series
ax.plot(time_series.times(), time_series.values(), '.-')
ax.grid()
ax.set_ylabel('Omega [rad/s]')

ax = axes[1]
time_series = drive.detuning.time_series
ax.plot(time_series.times(), time_series.values(), '.-')
ax.grid()
ax.set_ylabel('Delta [rad/s]')

ax = axes[2]
time_series = drive.phase.time_series
# Note: time series of phase is understood as a piecewise constant function
ax.step(time_series.times(), time_series.values(), '.-', where='post')
ax.set_ylabel('phi [rad]')
ax.grid()
ax.set_xlabel('time [s]')

plt.show()  # This will show the plot below in an ipython or jupyter session

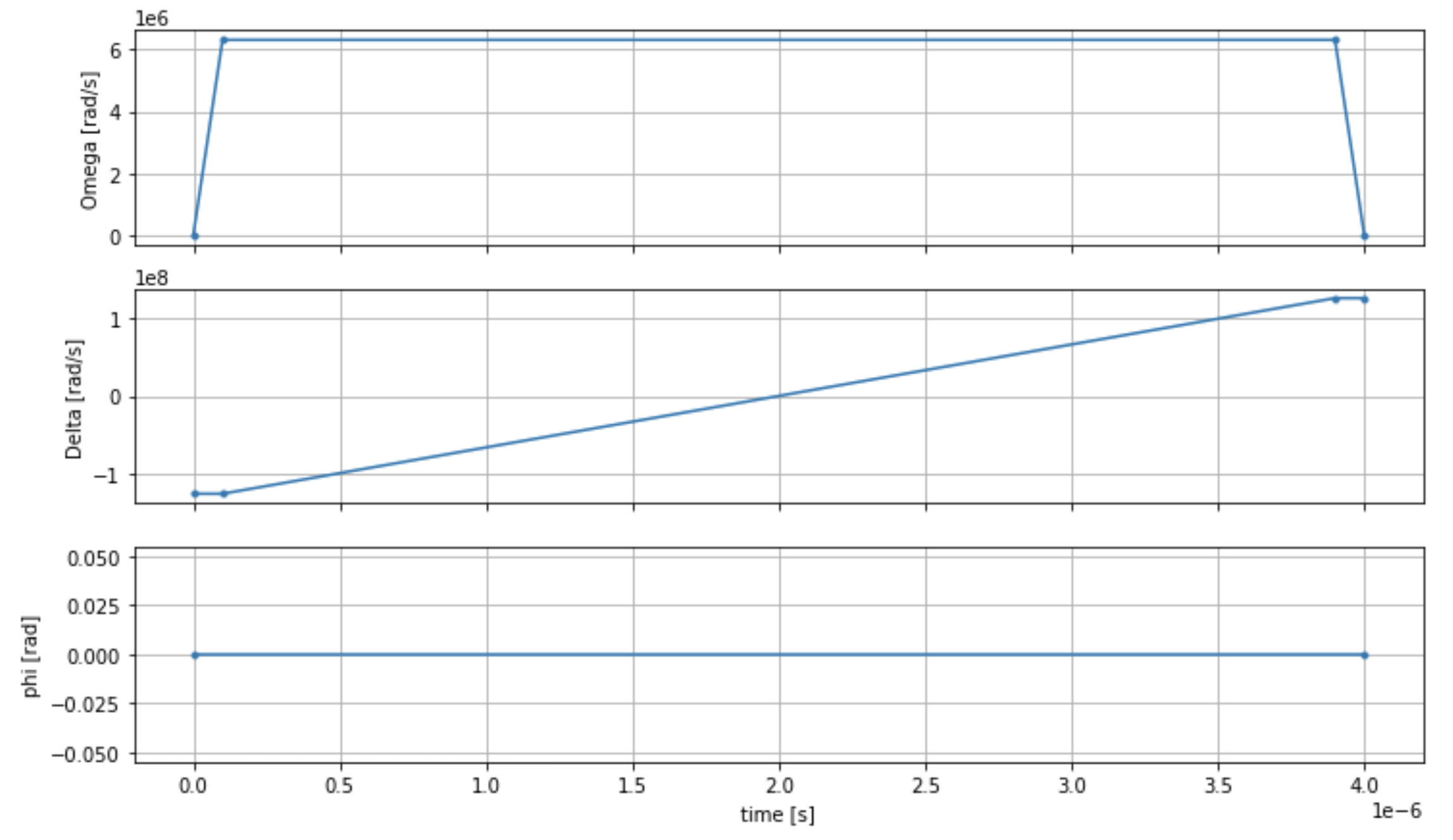
시간 경과에 따른 phi, delta 및 omega를 보여주는 세 가지 그래프입니다. 상단 서브플롯은 6rad/s를 약간 넘는 수준까지 증가한 후 4초 동안 유지되다가 다시 0으로 떨어지는 모습을 보여줍니다. 중간 서브플롯은 이에 상응하는 미분값의 선형 증가를 나타내며, 하단 서브플롯은 0에 가까운 평평한 선을 보여줍니다.

AHS 프로그램

레지스터, 구동장(및 암시적 van der Waals 상호 작용)은 아날로그 해밀토니안 시뮬레이션 프로그램 ahs_program을 구성합니다.


from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation

ahs_program = AnalogHamiltonianSimulation(
   register=register,
   hamiltonian=drive
)

로컬 시뮬레이터에서 실행

이 예제는 작기 때문에(스핀 수 15회 미만), AHS 호환 QPU에서 실행하기 전에 Braket SDK와 함께 제공되는 로컬 AHS 시뮬레이터에서 실행할 수 있습니다. Braket SDK를 통해 로컬 시뮬레이터를 무료로 사용할 수 있으므로, 이는 코드가 올바르게 실행될 수 있도록 보장하는 모범 사례입니다.

여기서는 로컬 시뮬레이터가 양자 상태의 시간 변화를 추적하고 최종 상태에서 샘플을 추출하므로 샷 수를 높은 값(예: 100만)으로 설정할 수 있습니다. 따라서 샷 수가 늘어나더라도 총 실행 시간은 약간만 증가합니다.


from braket.devices import LocalSimulator

device = LocalSimulator("braket_ahs")

result_simulator = device.run(
   ahs_program,
   shots=1_000_000
).result()  # Takes about 5 seconds

시뮬레이터 결과 분석

각 스핀의 상태("down"은 "d", "up"은 "u", 빈 위치는 "e"일 수 있음)를 추론하고 각 구성이 샷 전체에서 발생한 횟수를 계산하는 다음 함수를 사용하여 샷 결과를 집계할 수 있습니다.


from collections import Counter


def get_counts(result):
    """Aggregate state counts from AHS shot results

    A count of strings (of length = # of spins) are returned, where
    each character denotes the state of a spin (site):
      e: empty site
      u: up state spin
      d: down state spin

    Args:
      result (braket.tasks.analog_hamiltonian_simulation_quantum_task_result.AnalogHamiltonianSimulationQuantumTaskResult)

    Returns
       dict: number of times each state configuration is measured

    """
    state_counts = Counter()
    states = ['e', 'u', 'd']
    for shot in result.measurements:
        pre = shot.pre_sequence
        post = shot.post_sequence
        state_idx = np.array(pre) * (1 + np.array(post))
        state = "".join(map(lambda s_idx: states[s_idx], state_idx))
        state_counts.update((state,))
    return dict(state_counts)


counts_simulator = get_counts(result_simulator)  # Takes about 5 seconds
print(counts_simulator)


*[Output]*
{'dddddddd': 5, 'dddddddu': 12, 'ddddddud': 15, ...}

다음 counts는 샷 전체에서 각 상태 구성이 관찰된 횟수를 계산하는 딕셔너리입니다. 다음 코드로 시각화할 수도 있습니다.


from collections import Counter


def has_neighboring_up_states(state):
    if 'uu' in state:
        return True
    if state[0] == 'u' and state[-1] == 'u':
        return True
    return False


def number_of_up_states(state):
    return Counter(state)['u']


def plot_counts(counts):
    non_blockaded = []
    blockaded = []
    for state, count in counts.items():
        if not has_neighboring_up_states(state):
            collection = non_blockaded
        else:
            collection = blockaded
        collection.append((state, count, number_of_up_states(state)))

    blockaded.sort(key=lambda _: _[1], reverse=True)
    non_blockaded.sort(key=lambda _: _[1], reverse=True)

    for configurations, name in zip((non_blockaded,
                                     blockaded),
                                    ('no neighboring "up" states',
                                     'some neighboring "up" states')):
        plt.figure(figsize=(14, 3))
        plt.bar(range(len(configurations)), [item[1] for item in configurations])
        plt.xticks(range(len(configurations)))
        plt.gca().set_xticklabels([item[0] for item in configurations], rotation=90)
        plt.ylabel('shots')
        plt.grid(axis='y')
        plt.title(f'{name} configurations')
        plt.show()


plot_counts(counts_simulator)

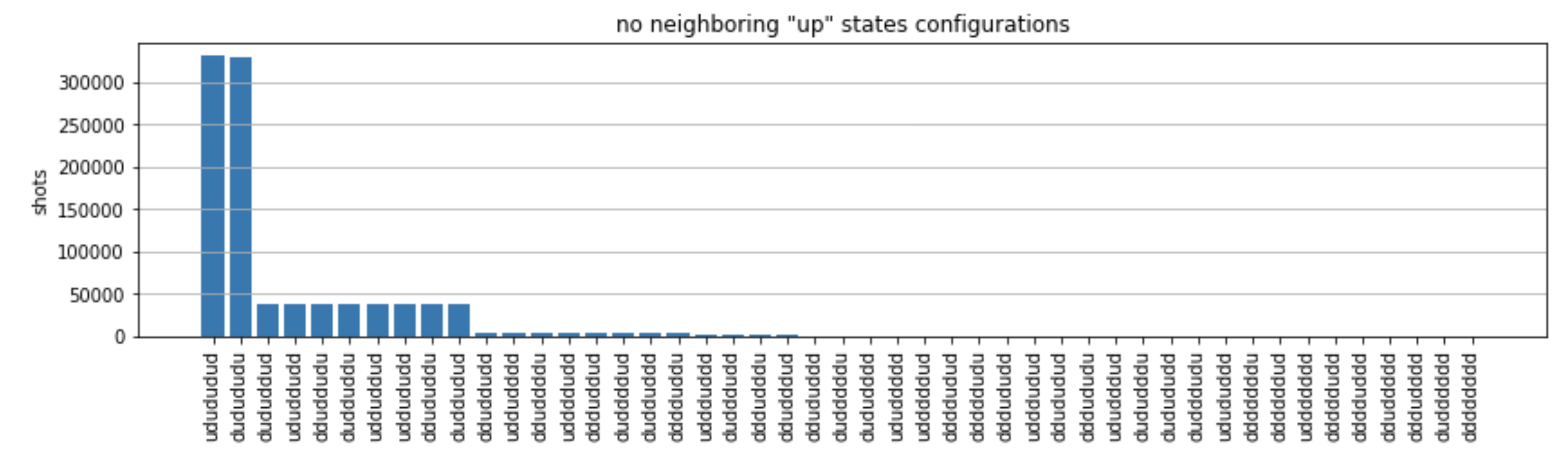
이웃하는 "up" 상태 구성이 없는 많은 수의 샷을 보여주는 막대 차트입니다.

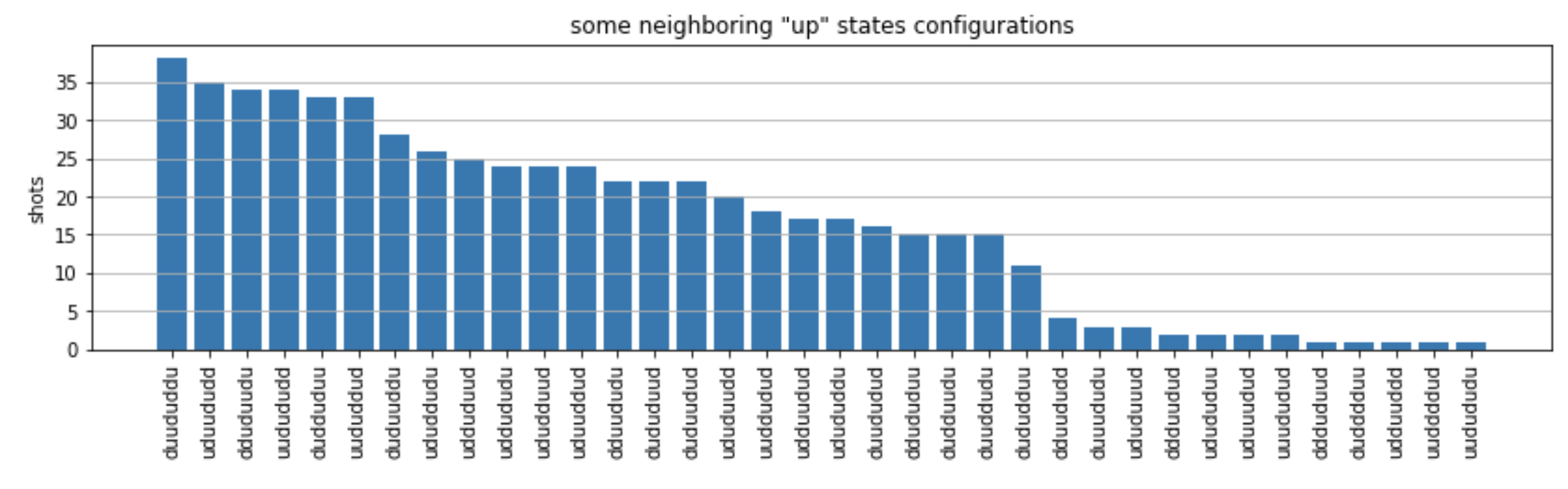
1.0 샷에 4개의 상태가 있는 일부 이웃하는 "up" 상태 구성의 샷을 보여주는 막대 차트입니다.

플롯에서 다음과 같은 관찰 가능 항목을 읽고 반강자성 위상을 성공적으로 준비했는지 확인할 수 있습니다.

일반적으로, 비차단 상태(두 개의 이웃하는 스핀이 “up” 상태에 있지 않음)는 하나 이상의 이웃하는 스핀 쌍이 모두 “up” 상태에 있는 상태보다 더 일반적입니다.
일반적으로 구성이 차단되지 않는 한 "up" 여기가 더 많은 상태가 선호됩니다.
가장 일반적인 상태는 실제로 완벽한 반강자성 상태 "dudududu" 및 "udududud"입니다.
두 번째로 일반적인 상태는 연속 분리가 1, 2, 2인 3개의 “up” 여기만 존재하는 상태입니다. 이는 van der Waals 상호 작용이 다음으로 가까운 이웃에도 (비록 훨씬 작지만) 영향을 미친다는 것을 보여줍니다.

QuEra의 Aquila QPU에서 실행

사전 조건: Braket SDK를 pip 설치하는 것 외에도, Amazon Braket을 처음 사용하는 경우 필요한 시작하기 단계를 완료했는지 확인합니다.

참고

Braket 호스팅 노트북 인스턴스를 사용하는 경우 Braket SDK는 인스턴스와 함께 사전 설치되어 제공됩니다.

모든 종속성이 설치된 상태에서 Aquila QPU에 연결할 수 있습니다.


from braket.aws import AwsDevice

aquila_qpu = AwsDevice("arn:aws:braket:us-east-1::device/qpu/quera/Aquila")

AHS 프로그램을 QuEra 시스템에 적합하게 만들려면 Aquila QPU에서 허용하는 정밀도 수준에 부합하도록 모든 값을 반올림해야 합니다. (이러한 요구 사항은 이름에 “분해능”이 있는 디바이스 파라미터에 의해 관리됩니다. 노트북에서 aquila_qpu.properties.dict()를 실행하면 확인할 수 있습니다. Aquila의 기능 및 요구 사항에 대한 자세한 내용은 Aquila 소개 노트북을 참조하세요.) discretize 메서드를 직접적으로 호출하여 이 작업을 수행할 수 있습니다.


discretized_ahs_program = ahs_program.discretize(aquila_qpu)

이제 Aquila QPU에서 프로그램(현재는 100회 샷만 실행)을 실행할 수 있습니다.

참고

Aquila 프로세서에서 이 프로그램을 실행하면 비용이 발생합니다. Amazon Braket SDK에는 고객이 비용 한도를 설정하고 거의 실시간으로 비용을 추적할 수 있는 Cost Tracker가 포함되어 있습니다.


task = aquila_qpu.run(discretized_ahs_program, shots=100)

metadata = task.metadata()
task_arn = metadata['quantumTaskArn']
task_status = metadata['status']

print(f"ARN: {task_arn}")
print(f"status: {task_status}")


*[Output]*
ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
status: CREATED

양자 작업 실행 시간은 가용성 창과 QPU 사용률에 따라 크게 달라질 수 있으므로, 양자 작업 ARN을 기록해 두는 것이 좋습니다. 그러면 나중에 다음 코드 조각을 사용하여 작업 상태를 확인할 수 있습니다.


# Optionally, in a new python session
from braket.aws import AwsQuantumTask

SAVED_TASK_ARN = "arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef"

task = AwsQuantumTask(arn=SAVED_TASK_ARN)
metadata = task.metadata()
task_arn = metadata['quantumTaskArn']
task_status = metadata['status']

print(f"ARN: {task_arn}")
print(f"status: {task_status}")


*[Output]*
ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
status: COMPLETED

상태가 COMPLETED(Amazon Braket 콘솔의 양자 작업 페이지에서도 확인할 수 있음)가 되면 다음을 사용하여 결과를 쿼리할 수 있습니다.


result_aquila = task.result()

QPU 결과 분석

이전과 동일한 get_counts 함수를 사용하여 개수를 계산할 수 있습니다.


counts_aquila = get_counts(result_aquila)
   print(counts_aquila)


*[Output]*
{'dddududd': 2, 'dudududu': 18, 'ddududud': 4, ...}

그리고 plot_counts로 플롯합니다.


plot_counts(counts_aquila)

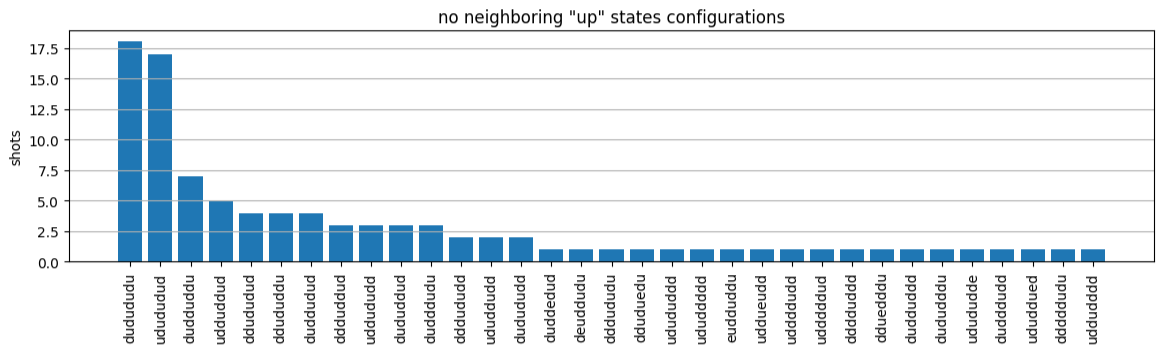
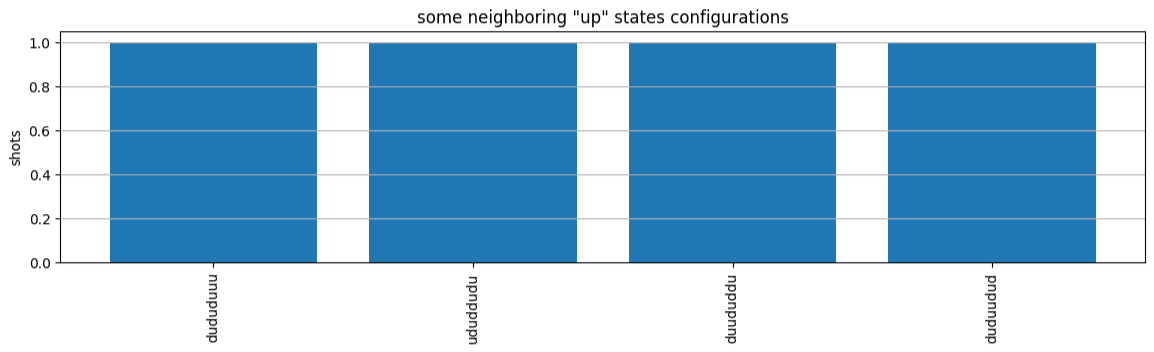
일부 샷에는 빈 위치("e"로 표시)가 있습니다. 이는 Aquila QPU의 원자당 1~2%에 달하는 준비 결함에 의한 것입니다. 이 외에도, 결과는 적은 샷 수로 인해 예상되는 통계적 변동 내에서 시뮬레이션과 일치합니다.

다음 단계

축하합니다, 이제 로컬 AHS 시뮬레이터와 Aquila QPU를 사용하여 Amazon Braket에서 첫 번째 AHS 워크로드를 실행하셨습니다.

Rydberg 물리학, 아날로그 해밀토니안 시뮬레이션 및 Aquila 디바이스에 대해 자세히 알아보려면 예제 노트북을 참조하세요.

javascript가 브라우저에서 비활성화되거나 사용이 불가합니다.

AWS 설명서를 사용하려면 Javascript가 활성화되어야 합니다. 지침을 보려면 브라우저의 도움말 페이지를 참조하십시오.

문서 규칙

(고급) 아날로그 해밀턴 시뮬레이션

QuEra Aquila를 사용하여 아날로그 프로그램 제출