翻訳は機械翻訳により提供されています。提供された翻訳内容と英語版の間で齟齬、不一致または矛盾がある場合、英語版が優先します。

Hello AHS: 初めてのアナログハミルトニアンシミュレーションを実行する

このセクションでは、初めてのアナログハミルトニアンシミュレーションの実行について説明します。

スピン鎖の操作

多くの相互作用パーティクルで構成される系の正規例については、8 つのスピンのリング (それぞれが「上向き」∣↑⟩ 状態と「下向き」∣↓⟩ 状態になる場合があります) を考えてみましょう。次のモデル系は小さいながらも、自然に発生する磁性物質によるいくつかの興味深い現象を最初から示しています。この例では、連続するスピンが反対方向に向く、いわゆる反強磁性秩序を作成する方法を示します。

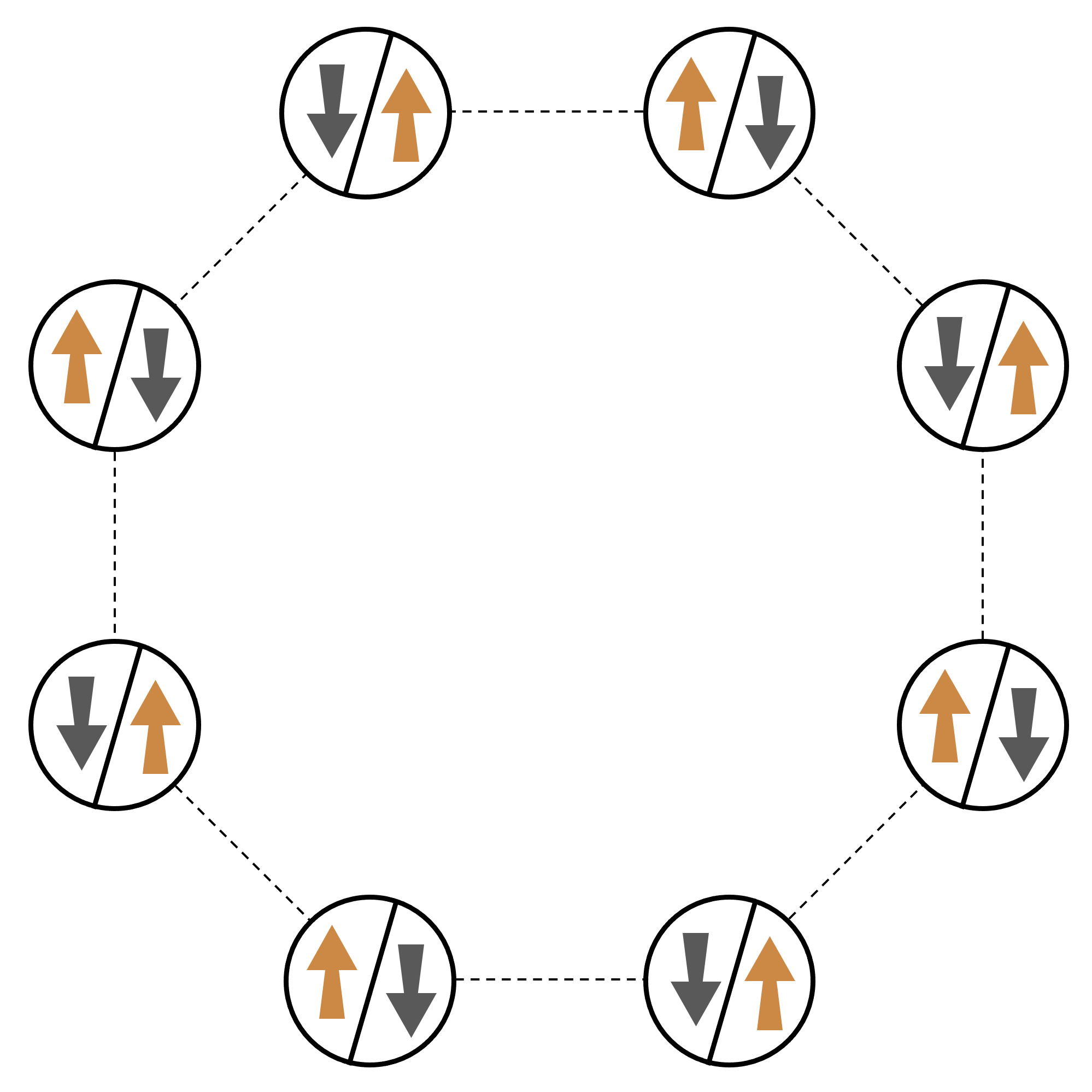
配置

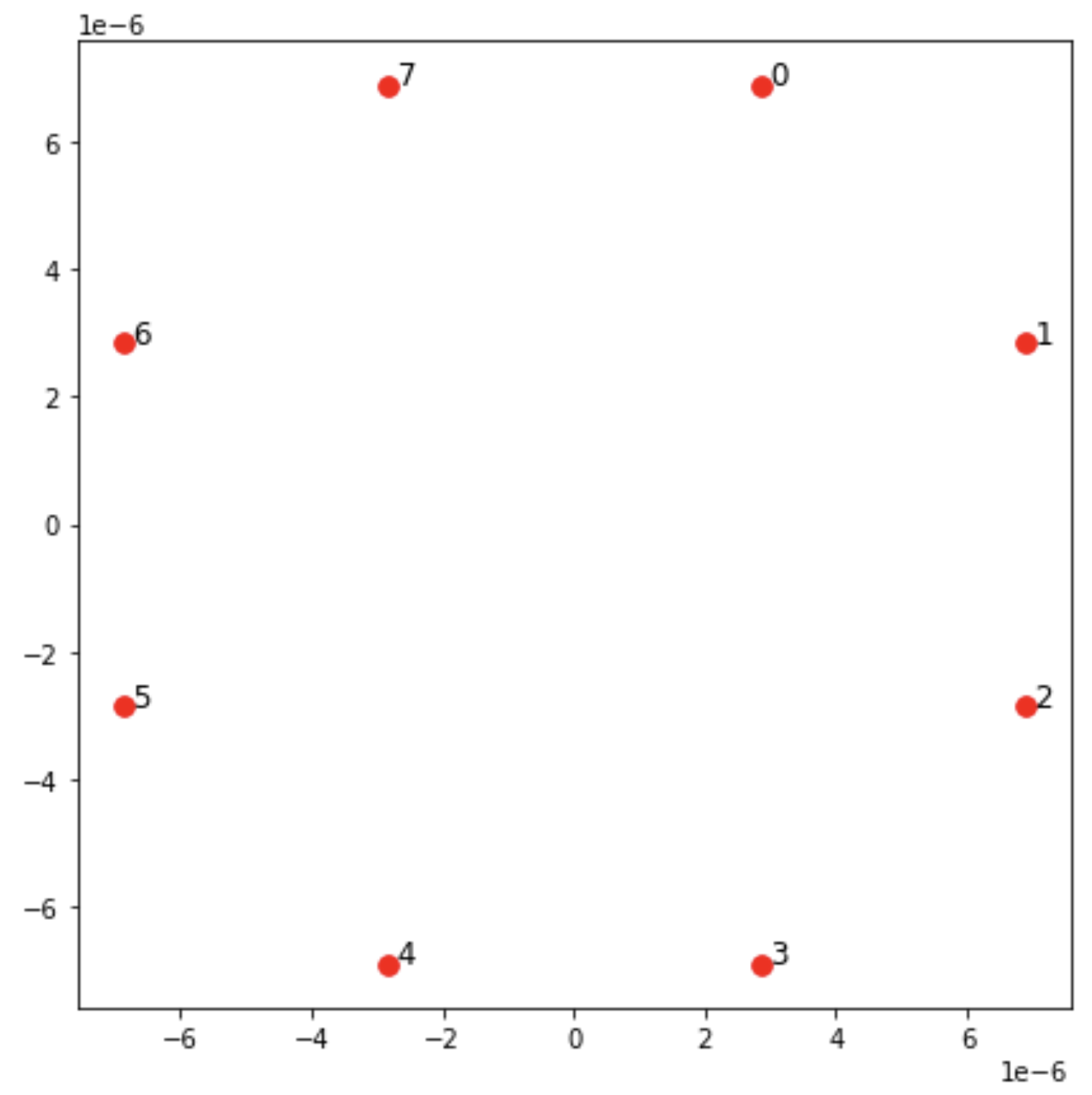
スピンごとに 1 つの中性原子を使用し、「上向き」スピン状態と「下向き」スピン状態をそれぞれ、原子の励起リュードベリ状態と基底状態でエンコードします。まず、2-d 配置を作成します。上記のスピンリングは、下記のコードでプログラミングできます。

前提条件: Braket SDK を pip install コマンドでインストールする必要があります。(Braket がホストするノートブックインスタンスを使用する場合には、そのノートブックはこの SDK にプリインストールされています)。プロットを再現する場合は、シェルコマンド pip install matplotlib を使用して matplotlib を別途インストールすることも必要です。

from braket.ahs.atom_arrangement import AtomArrangement
import numpy as np
import matplotlib.pyplot as plt  # Required for plotting

a = 5.7e-6  # Nearest-neighbor separation (in meters)

register = AtomArrangement()
register.add(np.array([0.5, 0.5 + 1/np.sqrt(2)]) * a)
register.add(np.array([0.5 + 1/np.sqrt(2), 0.5]) * a)
register.add(np.array([0.5 + 1/np.sqrt(2), - 0.5]) * a)
register.add(np.array([0.5, - 0.5 - 1/np.sqrt(2)]) * a)
register.add(np.array([-0.5, - 0.5 - 1/np.sqrt(2)]) * a)
register.add(np.array([-0.5 - 1/np.sqrt(2), - 0.5]) * a)
register.add(np.array([-0.5 - 1/np.sqrt(2), 0.5]) * a)
register.add(np.array([-0.5, 0.5 + 1/np.sqrt(2)]) * a)

これをプロットするには、以下を使用します。

fig, ax = plt.subplots(1, 1, figsize=(7, 7))
xs, ys = [register.coordinate_list(dim) for dim in (0, 1)]
ax.plot(xs, ys, 'r.', ms=15)

for idx, (x, y) in enumerate(zip(xs, ys)):
    ax.text(x, y, f" {idx}", fontsize=12)

plt.show()  # This will show the plot below in an ipython or jupyter session

相互作用

反強磁性相を作成するには、隣接するスピン間の相互作用を誘発する必要があります。これには ファンデルワールス相互作用を使用します。これは、中性原子デバイス (QuEra の Aquila デバイスなど) でネイティブに実装されています。この相互作用のハミルトニアン項は、スピン表現を使用することで、すべてのスピンペア (j,k) の和として表現できます。

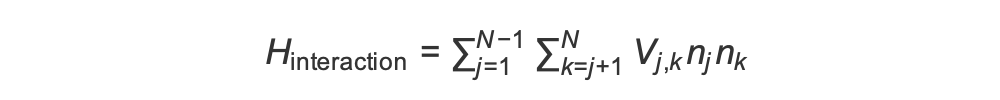
ここで、「nj​=∣↑_j​⟩⟨↑_j​∣ 」は、スピン j が「上向き」状態である場合にのみ値 1 を取り、それ以外の場合は 0 を取る演算子です。強度は V_j,k=C₆/(d_j,k​)⁶ です。C₆は固定係数、d_j,k はスピン j と k の間のユークリッド距離です。この相互作用項には、「スピン j とスピン k の両方が『上向き』であるすべての状態が、エネルギーを (V_j,k の量だけ) 増加させる」という即時効果があります。この相互作用に関する AHS プログラムの残りの部分を綿密に設計することで、隣接するスピンが両方とも「上向き」状態になるのを防ぐことができます。これは、一般的に「リュードベリ遮断」と呼ばれる効果です。

駆動場

AHS プログラムの開始時、すべてのスピン (デフォルト) は「下向き」状態で始まり、いわゆる強磁性相にあります。強磁性相を作成するという目的に留意し、スピンをこの状態から、「上向き」状態が望ましい多体状態にスムーズに遷移させる、時間依存のコヒーレント駆動場を指定します。対応するハミルトニアンは次のように記述できます。

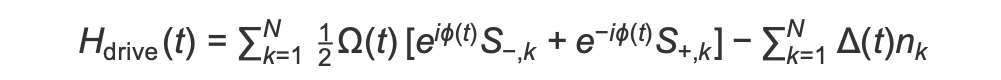
ここで、Ω(t)、ϕ(t)、Δ(t) はそれぞれ、すべてのスピンに均一に作用する駆動場に対する、時間依存、グローバル振幅 (別名: Rabi 周波数)、位相、およびデチューニングです。ここで、S_−,k=∣↓_k​⟩⟨↑_k​∣ および S_+,k=(S_−,k)^†=∣↑_k​⟩⟨↓_k​∣ はそれぞれ、スピン k の下降演算子と上昇演算子であり、n_k​=∣↑_k​⟩⟨↑_k​∣ は以前と同じ演算子です。駆動場において、Ω の項は、すべてのスピンの「下向き」状態と「上向き」状態を同時にコヒーレントに結合し、Δ の項は「上向き」状態のエネルギー報酬を制御します。

強磁性相から反強磁性相へのスムーズな遷移をプログラミングするには、駆動場を次のコードで指定します。

from braket.timings.time_series import TimeSeries
from braket.ahs.driving_field import DrivingField

# Smooth transition from "down" to "up" state
time_max = 4e-6  # seconds
time_ramp = 1e-7  # seconds
omega_max = 6300000.0  # rad / sec
delta_start = -5 * omega_max
delta_end = 5 * omega_max

omega = TimeSeries()
omega.put(0.0, 0.0)
omega.put(time_ramp, omega_max)
omega.put(time_max - time_ramp, omega_max)
omega.put(time_max, 0.0)

delta = TimeSeries()
delta.put(0.0, delta_start)
delta.put(time_ramp, delta_start)
delta.put(time_max - time_ramp, delta_end)
delta.put(time_max, delta_end)

phi = TimeSeries().put(0.0, 0.0).put(time_max, 0.0)

drive = DrivingField(
   amplitude=omega,
   phase=phi,
   detuning=delta
)

駆動場を時系列で図示するには、次のスクリプトを使用します。

fig, axes = plt.subplots(3, 1, figsize=(12, 7), sharex=True)

ax = axes[0]
time_series = drive.amplitude.time_series
ax.plot(time_series.times(), time_series.values(), '.-')
ax.grid()
ax.set_ylabel('Omega [rad/s]')

ax = axes[1]
time_series = drive.detuning.time_series
ax.plot(time_series.times(), time_series.values(), '.-')
ax.grid()
ax.set_ylabel('Delta [rad/s]')

ax = axes[2]
time_series = drive.phase.time_series
# Note: time series of phase is understood as a piecewise constant function
ax.step(time_series.times(), time_series.values(), '.-', where='post')
ax.set_ylabel('phi [rad]')
ax.grid()
ax.set_xlabel('time [s]')

plt.show()  # This will show the plot below in an ipython or jupyter session

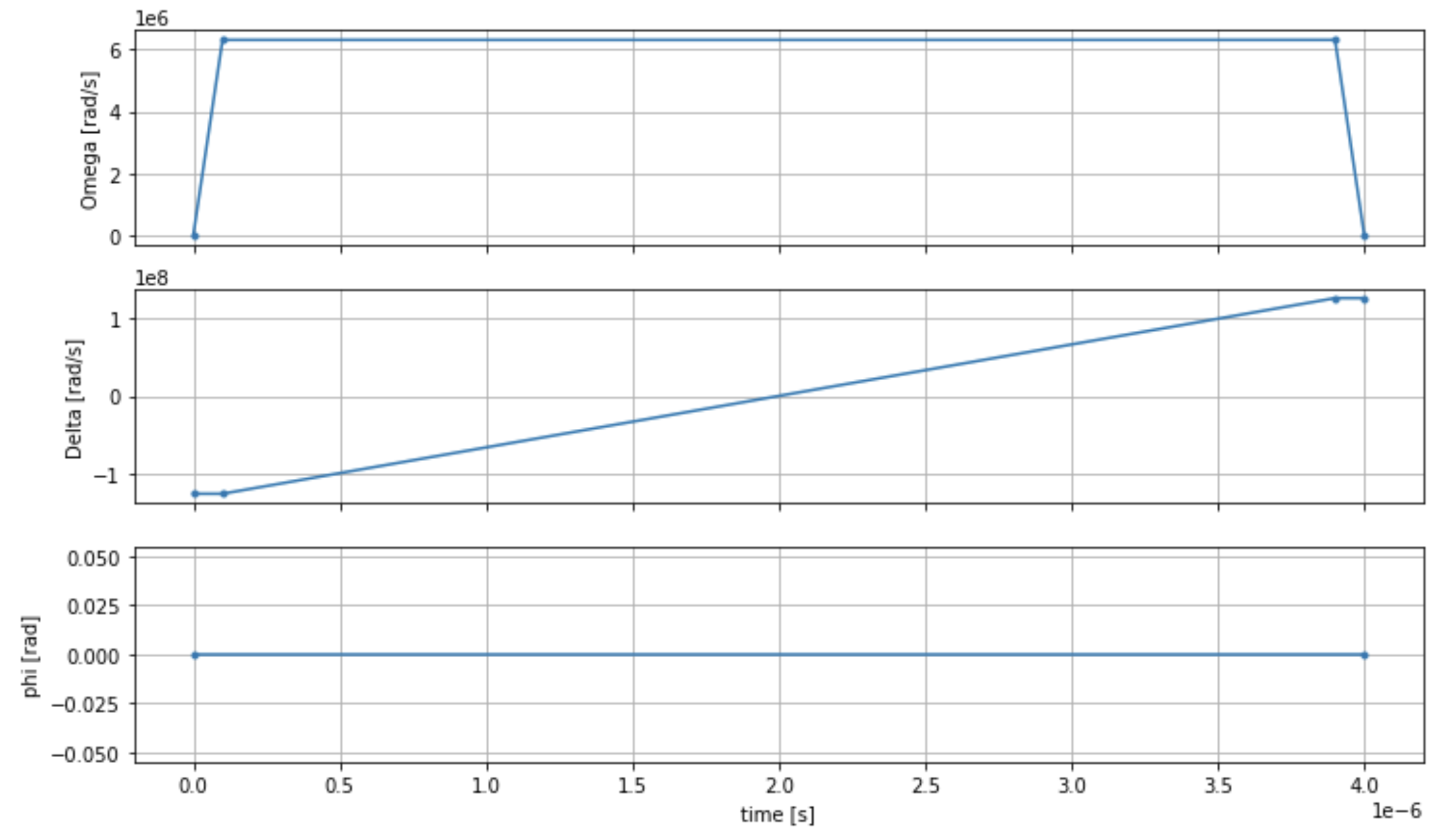
AHS プログラム

アナログハミルトニアンシミュレーションプログラム ahs_program は、レジスタと駆動場 (および暗黙のファンデルワールス相互作用) で構成されています。

from braket.ahs.analog_hamiltonian_simulation import AnalogHamiltonianSimulation

ahs_program = AnalogHamiltonianSimulation(
   register=register,
   hamiltonian=drive
)

ローカルシミュレーターでの実行

この例は小規模 (15 スピン未満) のため、AHS 互換 QPU で実行する前に、Braket SDK に付属のローカル AHS シミュレーターで実行できます。このローカルシミュレーターは、Braket SDK で無償で利用できるため、コードが正しく実行されるかを確認するためのベストプラクティスです。

ここでは、ショットの数を高い値 (例えば、100 万) に設定できます。量子状態の時間進化を追跡し、最終状態からサンプルを描画するのが、ローカルシミュレーターであるためです。つまり、ショットの数を増やしても、全体のランタイムはわずかに長くなるだけで済みます。

from braket.devices import LocalSimulator

device = LocalSimulator("braket_ahs")

result_simulator = device.run(
   ahs_program,
   shots=1_000_000
).result()  # Takes about 5 seconds

シミュレーター結果の分析

各スピンの状態 (「下向き」の場合は「d」、「上向き」の場合は「u」、空のサイトの場合は「e」) を推測する次の関数を使用して、ショット結果を集計し、各設定がショット全体で発生した回数をカウントできます。

from collections import Counter


def get_counts(result):
    """Aggregate state counts from AHS shot results

    A count of strings (of length = # of spins) are returned, where
    each character denotes the state of a spin (site):
      e: empty site
      u: up state spin
      d: down state spin

    Args:
      result (braket.tasks.analog_hamiltonian_simulation_quantum_task_result.AnalogHamiltonianSimulationQuantumTaskResult)

    Returns
       dict: number of times each state configuration is measured

    """
    state_counts = Counter()
    states = ['e', 'u', 'd']
    for shot in result.measurements:
        pre = shot.pre_sequence
        post = shot.post_sequence
        state_idx = np.array(pre) * (1 + np.array(post))
        state = "".join(map(lambda s_idx: states[s_idx], state_idx))
        state_counts.update((state,))
    return dict(state_counts)


counts_simulator = get_counts(result_simulator)  # Takes about 5 seconds
print(counts_simulator)

*[Output]*
{'dddddddd': 5, 'dddddddu': 12, 'ddddddud': 15, ...}

ここで、counts は、ショット全体で各状態設定が観測された回数をカウントするディクショナリです。また、この回数を視覚化するには、次のコードを使用します。

from collections import Counter


def has_neighboring_up_states(state):
    if 'uu' in state:
        return True
    if state[0] == 'u' and state[-1] == 'u':
        return True
    return False


def number_of_up_states(state):
    return Counter(state)['u']


def plot_counts(counts):
    non_blockaded = []
    blockaded = []
    for state, count in counts.items():
        if not has_neighboring_up_states(state):
            collection = non_blockaded
        else:
            collection = blockaded
        collection.append((state, count, number_of_up_states(state)))

    blockaded.sort(key=lambda _: _[1], reverse=True)
    non_blockaded.sort(key=lambda _: _[1], reverse=True)

    for configurations, name in zip((non_blockaded,
                                     blockaded),
                                    ('no neighboring "up" states',
                                     'some neighboring "up" states')):
        plt.figure(figsize=(14, 3))
        plt.bar(range(len(configurations)), [item[1] for item in configurations])
        plt.xticks(range(len(configurations)))
        plt.gca().set_xticklabels([item[0] for item in configurations], rotation=90)
        plt.ylabel('shots')
        plt.grid(axis='y')
        plt.title(f'{name} configurations')
        plt.show()


plot_counts(counts_simulator)

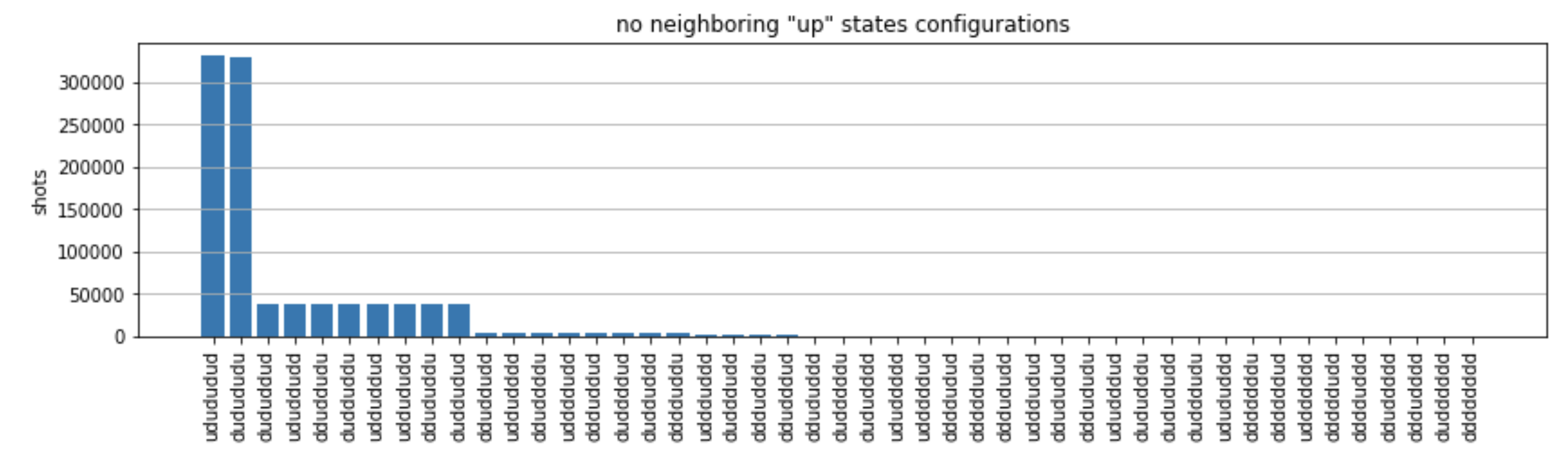
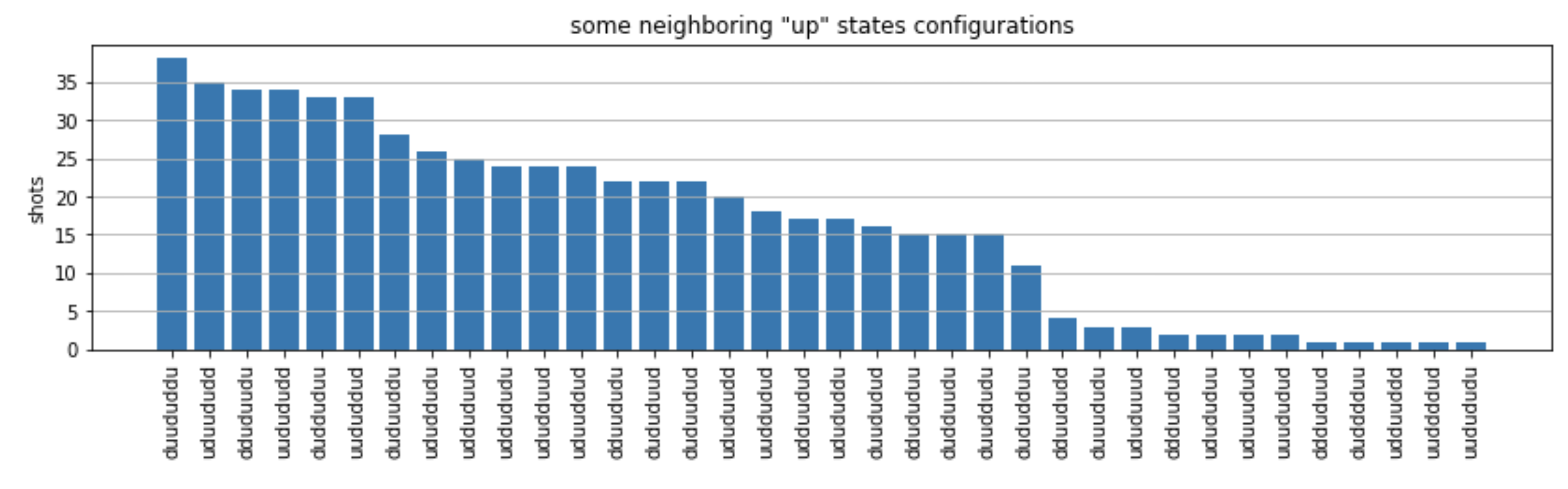
プロットから、以下の観測値を読み取ることで、反強磁性相が作成されたことを確認できます。

QuEra Aquila QPU での実行

前提条件: Amazon Braket を初めて使用する場合 (Braket SDK を pip install コマンドでインストールすることは除く) は、必要な開始手順を完了していることを確認してください。

すべての依存関係をインストールすると、Aquila QPU に接続できます。

from braket.aws import AwsDevice

aquila_qpu = AwsDevice("arn:aws:braket:us-east-1::device/qpu/quera/Aquila")

AHS プログラムを QuEra マシンに適したものにするには、Aquila QPU で許容される精度レベルに準拠するようにすべての値を丸める必要があります。(丸める必要があるかどうかは、名前に「Resolution」が含まれるデバイスパラメータで管理されています。そのようなデバイスパラメータを確認するには、ノートブックで aquila_qpu.properties.dict() を実行します。Aquila の機能と要件の詳細については、「Introduction to Aquila」ノートブックを参照してください)。丸めるには、discretize メソッドを呼び出します。

discretized_ahs_program = ahs_program.discretize(aquila_qpu)

これで、プログラムを Aquila QPU で実行 (現在、100 ショットのみを実行) できるようになりました。

task = aquila_qpu.run(discretized_ahs_program, shots=100)

metadata = task.metadata()
task_arn = metadata['quantumTaskArn']
task_status = metadata['status']

print(f"ARN: {task_arn}")
print(f"status: {task_status}")

*[Output]*
ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
status: CREATED

量子タスクの実行にかかる時間は可用性ウィンドウと QPU 使用率によって大きなばらつきがあるため、後で次のコードスニペットを使用して量子タスク ARN の状態を確認できるように、ARN を書き留めておくことをお勧めします。

# Optionally, in a new python session
from braket.aws import AwsQuantumTask

SAVED_TASK_ARN = "arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef"

task = AwsQuantumTask(arn=SAVED_TASK_ARN)
metadata = task.metadata()
task_arn = metadata['quantumTaskArn']
task_status = metadata['status']

print(f"ARN: {task_arn}")
print(f"status: {task_status}")

*[Output]*
ARN: arn:aws:braket:us-east-1:123456789012:quantum-task/12345678-90ab-cdef-1234-567890abcdef
status: COMPLETED

状態が [完了] になる (Amazon Braket コンソールの量子タスクページから確認できます) と、以下を使用してタスクの結果をクエリできます。

result_aquila = task.result()

QPU の結果を分析する

カウントを計算するには、以前と同じ get_counts 関数を使用します。

counts_aquila = get_counts(result_aquila)
   print(counts_aquila)

*[Output]*
{'dddududd': 2, 'dudududu': 18, 'ddududud': 4, ...}

次に、カウントをプロットするには、plot_counts を使用します。

plot_counts(counts_aquila)

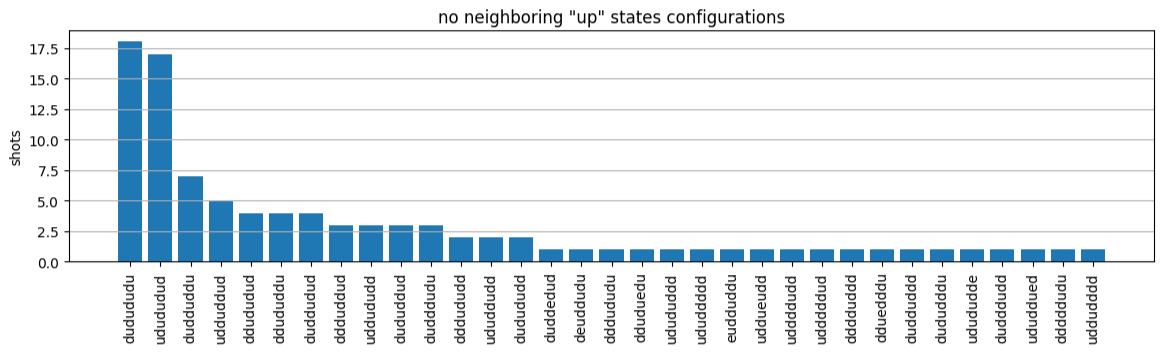
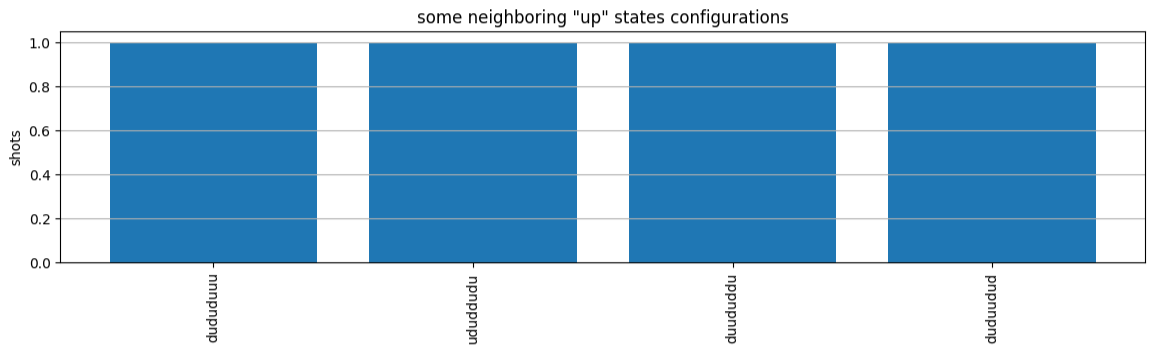
ショットのごく一部に空のサイトがあることに注意してください (「e」でマークされています)。これは、Aquila QPU の原子ごとの準備の不完全性が 1～2% であるためです。これを例外とすれば、結果は、シミュレーションと、ショット数が少ないことによる予想される統計的変動の範囲内で一致しています。

次の手順

これで、ローカル AHS シミュレーターと Aquila QPU を使用して Amazon Braket で初めての AHS ワークロードを実行できました。

リュードベリ物理学、アナログハミルトニアンシミュレーション、Aquila デバイスの詳細については、example ノートブックを参照してください。