Die vorliegende Übersetzung wurde maschinell erstellt. Im Falle eines Konflikts oder eines Widerspruchs zwischen dieser übersetzten Fassung und der englischen Fassung (einschließlich infolge von Verzögerungen bei der Übersetzung) ist die englische Fassung maßgeblich.

Fallstudie

In diesem Abschnitt werden ein reales Geschäftsszenario und eine Anwendung zur Quantifizierung von Unsicherheiten in Deep-Learning-Systemen untersucht. Angenommen, Sie möchten, dass ein Modell für maschinelles Lernen automatisch beurteilt, ob ein Satz grammatikalisch inakzeptabel (negativer Fall) oder akzeptabel (positiver Fall) ist. Stellen Sie sich den folgenden Geschäftsprozess vor: Wenn das Modell einen Satz als grammatikalisch akzeptabel (positiv) kennzeichnet, verarbeiten Sie ihn automatisch, ohne menschliche Überprüfung. Wenn das Modell den Satz als inakzeptabel (negativ) kennzeichnet, geben Sie den Satz zur Überprüfung und Korrektur an einen Menschen weiter. In der Fallstudie werden tiefe Ensembles zusammen mit Temperaturskalierung verwendet.

Dieses Szenario hat zwei Geschäftsziele:

Basis-Ergebnisse

Wenn ein einzelnes Modell auf die Daten angewendet wird, ohne dass es zum Testzeitpunkt zu einem Ausfall kam, ergeben sich folgende Ergebnisse:

Das Modell weist bei negativen Proben eine wesentlich geringere Leistung auf. Bei Geschäftsanwendungen sollte jedoch der Rückruf negativer Proben die wichtigste Kennzahl sein.

Anwendung tiefer Ensembles

Um die Modellunsicherheit zu quantifizieren, haben wir die Standardabweichungen einzelner Modellvorhersagen über tiefe Ensembles hinweg verwendet. Unsere Hypothese ist, dass wir für falsch positive (FP) und falsch negative Ergebnisse (FN) erwarten, dass die Unsicherheit viel höher sein wird als für echte positive (TP) und echte negative Ergebnisse (TN). Insbesondere sollte das Modell eine hohe Zuverlässigkeit haben, wenn es richtig ist, und ein niedriges Vertrauen, wenn es falsch ist, sodass wir anhand der Unsicherheit sagen können, wann wir der Leistung des Modells vertrauen können.

Die folgende Konfusionsmatrix zeigt die Unsicherheitsverteilung zwischen den FN-, FP-, TN- und TP-Daten. Die Wahrscheinlichkeit einer negativen Standardabweichung ist die Standardabweichung der Wahrscheinlichkeit negativer Werte in allen Modellen. Der Median, der Mittelwert und die Standardabweichungen werden im gesamten Datensatz aggregiert.

Wie die Matrix zeigt, schnitt das Modell bei TP am besten ab, sodass es die geringste Unsicherheit aufweist. Das Modell schnitt bei FP am schlechtesten ab, sodass es die höchste Unsicherheit aufweist, was unserer Hypothese entspricht.

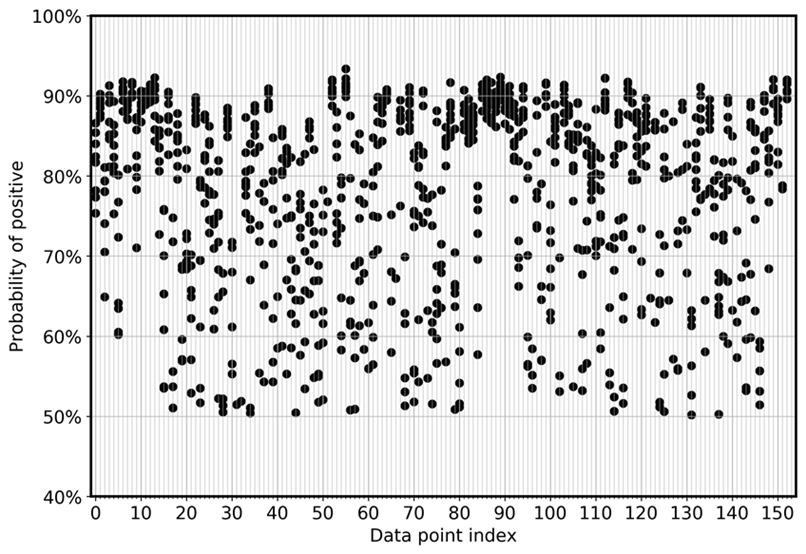
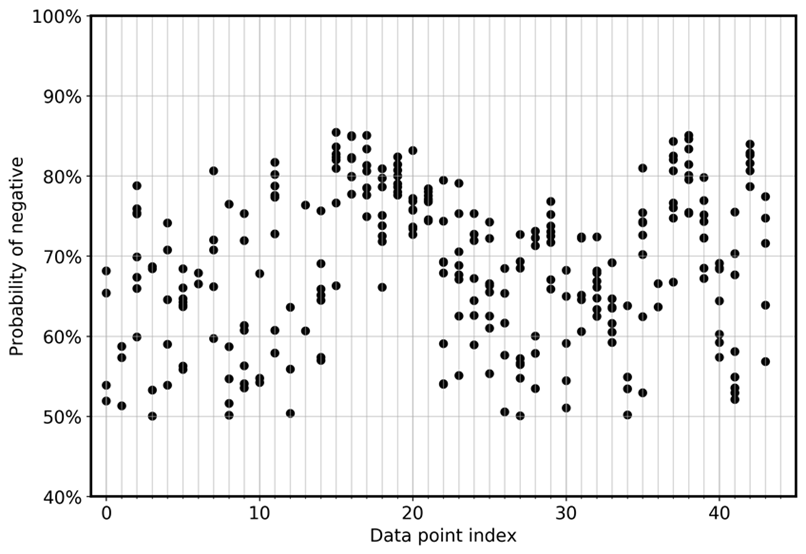
Um die Abweichung des Modells zwischen den Ensembles direkt zu visualisieren, zeigt das folgende Diagramm die Wahrscheinlichkeit in einer Streuansicht für FN und FP für die CoLA-Daten. Jede vertikale Linie steht für eine bestimmte Eingabestichprobe. Die Grafik zeigt acht Ensemble-Modellansichten. Das heißt, jede vertikale Linie hat acht Datenpunkte. Diese Punkte überlappen sich entweder perfekt oder sind in einem Bereich verteilt.

Das erste Diagramm zeigt, dass sich die Wahrscheinlichkeit FPs, positiv zu sein, für alle acht Modelle des Ensembles zwischen 0,5 und 0,925 verteilt.

In ähnlicher Weise zeigt die nächste Grafik, dass sich die Wahrscheinlichkeit FNs, negativ zu sein, bei den acht Modellen des Ensembles zwischen 0,5 und 0,85 verteilt.

Definition einer Entscheidungsregel

Um den Nutzen der Ergebnisse zu maximieren, verwenden wir die folgende Ensemble-Regel: Für jede Eingabe verwenden wir das Modell, das die geringste Wahrscheinlichkeit hat, positiv (akzeptabel) zu sein, um wichtige Entscheidungen zu treffen. Wenn die gewählte Wahrscheinlichkeit größer oder gleich dem Schwellenwert ist, kennzeichnen wir den Fall als akzeptabel und verarbeiten ihn automatisch. Andernfalls senden wir den Fall zur Überprüfung durch einen Mitarbeiter. Dies ist eine konservative Entscheidungsregel, die in stark regulierten Umgebungen angemessen ist.

Auswertung der Ergebnisse

Die folgende Grafik zeigt die Genauigkeit, das Erinnerungsvermögen und die auto (Automatisierungs-) Rate für negative Fälle (Fälle mit Grammatikfehlern). Die Automatisierungsrate bezieht sich auf den Prozentsatz der Fälle, die automatisch bearbeitet werden, weil das Modell den Satz als akzeptabel kennzeichnet. Ein perfektes Modell mit 100% iger Wiedererkennbarkeit und Präzision würde eine Automatisierungsrate von 69% (positive Fälle/Gesamtzahl der Fälle) erreichen, da nur positive Fälle automatisch bearbeitet werden.

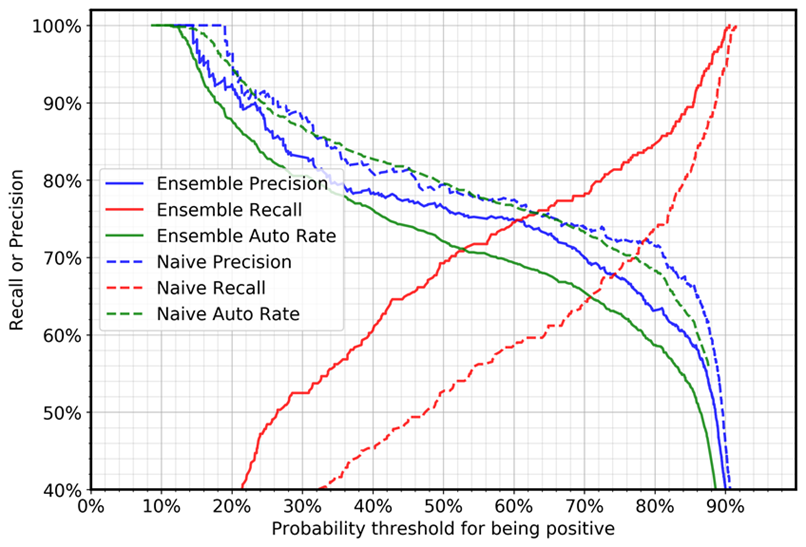
Der Vergleich zwischen Deep-Ensemble-Fällen und naiven Fällen zeigt, dass bei derselben Schwellenwerteinstellung der Erinnerungswert ziemlich drastisch zunimmt und die Präzision leicht abnimmt. (Die Automatisierungsrate hängt vom positiven und negativen Stichprobenverhältnis im Testdatensatz ab.) Zum Beispiel:

Sie können sehen, dass Deep Ensemble bestimmte Kennzahlen (in unserem Fall die Erinnerung an negative Fälle) für Geschäftsanwendungen verbessern kann, ohne dass die Größe der Trainingsdaten, ihre Qualität oder die Methode des Modells erhöht werden müssen.